What is a vector?

Before discussing the basic operations of vectors, let’s first think about what a vector is.

1) A vector is like an arrow

First and foremost, a vector can be defined as a value defined by its magnitude and direction in physics.

This definition reflects the geometric properties of vectors well, particularly the invariance of a vector’s coordinate system transformation.

The invariance of a vector with respect to a coordinate system transformation means that, as shown in the figure below, the vector itself remains unchanged even as the coordinate system changes.

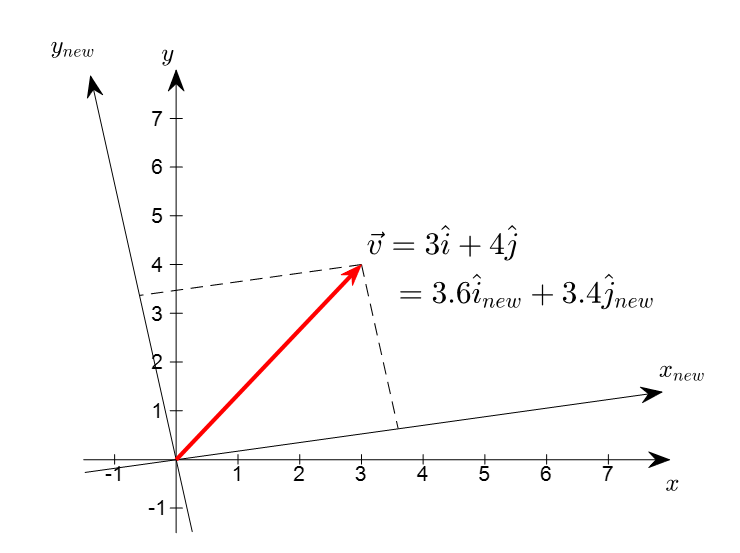
Figure 1. Coordinate system transformation and vectors. The vector remains unchanged even as the coordinate system changes, but its components change.

It should be noted that this description of a vector as a value defined by its magnitude and direction is only applicable to Euclidean vectors.

However, this definition is useful for visualizing vectors, so unless otherwise stated, Euclidean vectors will be used for visualization.

2) A vector is a list of numbers in order

Another way to think about vectors is as a list of numbers arranged in a specific order.

This perspective is very useful when considering vectors as a single data point.

Additionally, this perspective allows for an infinite number of dimensions without much difficulty - simply adding more numbers to the list creates a higher-dimensional vector.

This perspective also illustrates the fact that vector components are variable with respect to coordinate system transformations.

To better understand what it means for vector components to be variable, let’s take another look at Figure 1.

In Figure 1, the vector is represented in two different coordinate systems, and even though the vector remains stationary, the coordinates representing the vector change as the viewing coordinate system changes.

3) A vector is an element of a vector space

While the above two definitions are useful, the most meaningful mathematical definition of a vector is simply that it is an element of a vector space.

This definition is similar to defining a university student as someone who attends a university - those who understand what a university is will understand the definition immediately, but for those who don’t, it may seem like a circular definition.

Defining vectors in this way emphasizes that any object with these characteristics can be treated as a vector and manipulated accordingly.

For instance, various techniques can be applied to apply the concept of vectors to seemingly non-vector concepts such as functions or matrices, which allows for their application in different contexts.

We will cover more about vector spaces in the future, but a vector space must have three defined and established elements:

\[(V, +, \cdot)\]

Here, $V$ represents the vector, $+$ represents the addition rule, and $\cdot$ represents the multiplication rule ¹.

Although it may seem overly abstract and ambiguous at this point, this level of abstraction allows for the concept of vectors to be extended to a wider range of applications and can be used to explain many occurrences in the world of linear algebra.

Basic Operations of Vectors

In reality, the basic operations of vectors are quite simple.

There are only two basic operations for vectors: scalar multiplication and vector addition.

Scalar Multiplication of Vectors

For any arbitrary set $V(\neq \phi)$, for any vector $x\in V$ and scalar $k\in {\Bbb R}$, the following must be satisfied:

\[x\in V, k\in {\Bbb R} \Rightarrow kx\in V\]

To explain this visually, we can think of the given arrow as representing a change in size (either increasing or decreasing) corresponding to a scalar value.

Figure 2. Vector in a 2-dimensional real space that increases or decreases in size corresponding to various scalar values

Vector Addition

For any arbitrary set $V(\neq \phi)$, for any vectors $x, y\in V$, the following must be satisfied:

\[x, y\in V, \Rightarrow x+y\in V\]

Visually, we can think of adding the sizes and directions of two given arrows together to create a parallelogram-shaped vector.

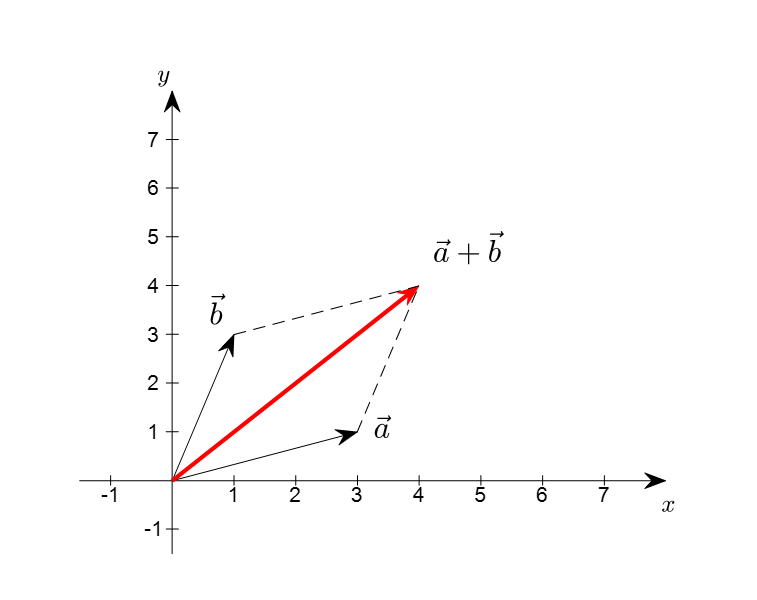
Figure 3. The sum of two vectors $\vec{a}$ and $\vec{b}$, denoted as $\vec{a}+\vec{b}$.

To elaborate a little, there is a slight difference between the vectors in physics and the vectors in mathematics. In mathematics, all vectors should have their starting point at the origin.

Importance of Scalar Multiplication and Vector Addition

Basically, the importance of scalar multiplication and vector addition is that when these two operations are well-defined entities, they satisfy linearity.

We will deal with linearity gradually, but in short, we can say that concepts that satisfy linearity are mathematically easy to handle, so we try to find and study concepts that satisfy linearity.

If we look at the concepts that will be covered in the future, which are based on scalar multiplication and vector addition, we can consider the following:

The Most Basic Data Transformation Method

From the perspective of “a vector is a sequence of numbers arranged in order,” which is the second perspective on vectors mentioned above, scalar multiplication and vector addition can be important.

That is, it is an application of viewing data as vectors and processing the data in that way.

For example, let’s say we are calculating the average scores of five people in Korean and English.

If we represent the scores in Korean as a vector, it can be as follows:

\[k = \begin{bmatrix}100\\70\\30\\45\\80\end{bmatrix}\]

Also, if we represent the scores in English as a vector, it can be as follows:

\[e = \begin{bmatrix}83\\50\\25\\30\\60\end{bmatrix}\]

Then, the method of grading the average of the two scores would be as follows:

\[avg = \frac{1}{2}k + \frac{1}{2}e = \frac{1}{2}\begin{bmatrix}100\\70\\30\\45\\80\end{bmatrix}+\frac{1}{2}\begin{bmatrix}83\\50\\25\\30\\60\end{bmatrix}\]

Although we have provided an example of a simple average, we would like to emphasize that many data processing techniques, such as PCA, SVD, linear regression, independent component analysis, and so on, are based on viewing data as vectors and processing them accordingly.

Linear Combination of Vectors

Fundamentally, scalar multiplication and vector addition are essential concepts for expressing linear combinations of vectors.

By utilizing scalar multiplication and vector addition together, we can express linear combinations of any two arbitrary vectors, as shown in the following example:

\[\Rightarrow c_1\begin{bmatrix}1\\0 \end{bmatrix}+c_2\begin{bmatrix}0\\1 \end{bmatrix}\]

The term “linear combination” may sound difficult, but it is actually a combination of scalar multiplication and vector addition expressed together.

So why is this simple concept of scalar multiplication and vector addition so important in linear algebra?

In the example above, $c_1$ and $c_2$ can correspond to any real number, and the resulting linear combination obtained by changing $c_1$ and $c_2$ corresponds to all vectors in the two-dimensional real vector space.

Figure 4. Vectors in the two-dimensional real space corresponding to various $c_1$ and $c_2$

This concept of linear combinations of vectors corresponding to the entire vector space is called span, and it provides an important clue for obtaining a new perspective on the process of obtaining the solutions of systems of linear equations through matrix multiplication.