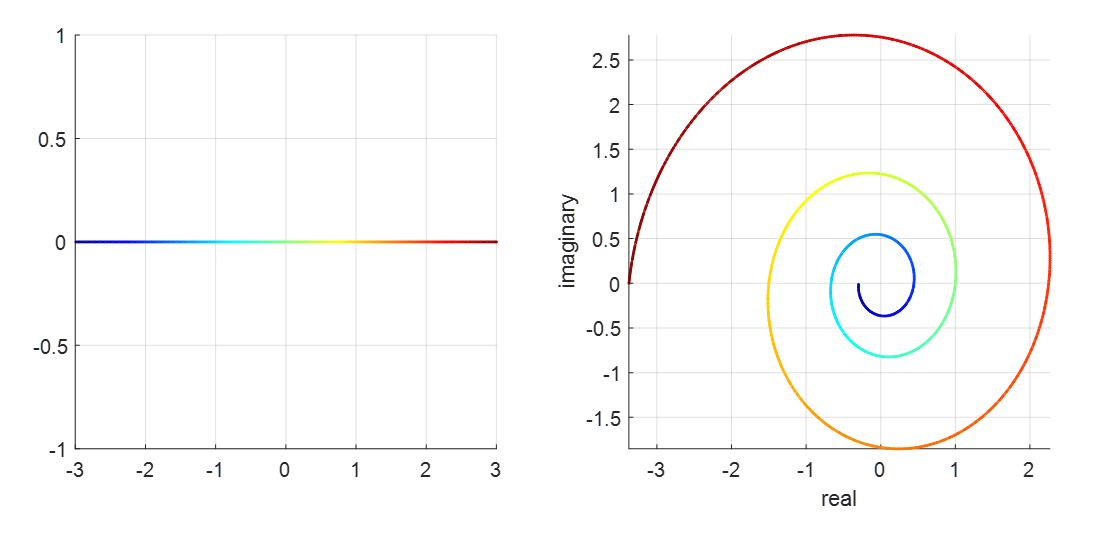
Exponential function with negative base $y = (-1.5)^x$. The left plot represents the domain, and the right plot represents the range.

※ In this article, we assume that complex numbers are single-valued.

Definition of Exponential Functions

Exponential functions are typically defined for positive bases. According to Wikipedia, exponential functions are defined as follows:

DEFINITION 1. Exponential Function
Given a positive constant $a$ and a variable $x$ that can take any real value, $$y = a^x$$is called an exponential function.

A common visualization of exponential functions is shown below:

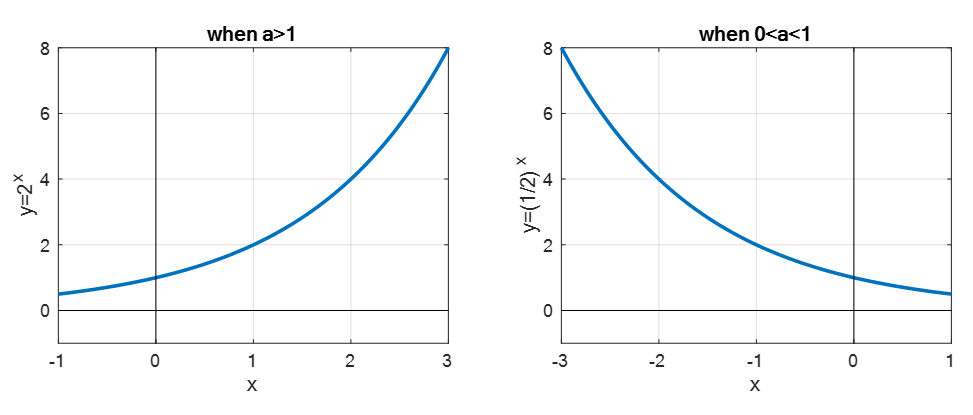
Figure 1. Typical exponential functions with bases greater than 1 and between 0 and 1.

But what about exponential functions with negative bases and real exponents?

For example, even for the case of $y = (-1)^x$, it is relatively easy to handle when $x$ is an integer using the definition of multiplication. However, when the exponent $x$ is a real number, it becomes more challenging to determine the value of the function.

However, upon closer inspection, we know that for $y = (-1)^{1/2}$, the value is the imaginary unit $i$. This suggests that we might be able to find solutions for exponential functions with negative bases in the complex number domain.

Understanding Numbers: Magnitude and Direction

Numbers with left and right direction: Integers

To consider exponential functions with negative bases, we need to further understand negative numbers.

Negative numbers can be decomposed into magnitude and direction, as shown in the following Figure 2:

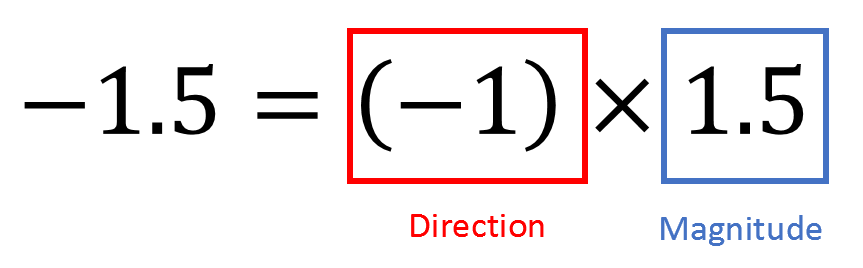
Figure 2. Negative numbers have both magnitude and direction.

Figure 3. Animation showing the direction and magnitude of -1.5 in the complex plane.

Complex Numbers: Numbers with Direction in the 2D Plane

However, direction does not have to be limited to just left or right. In a 2D plane, there can be numerous directions such as up, down, left, right, and many others, spanning 360 degrees. In other words, numbers (referred to as complex numbers here) can have both magnitude and direction.

To represent all directions on a 2D plane, we just need two orthogonal directions. As mentioned in the previous article on imaginary numbers ¹, imaginary numbers are a system of numbers orthogonal to real numbers, so by introducing the real axis and imaginary axis, we can represent complex numbers in a 2D plane.

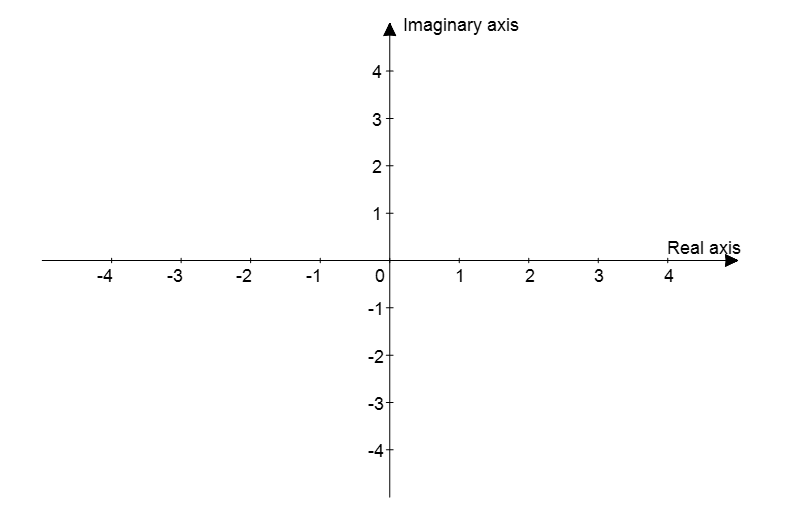
Figure 4. Complex plane constructed using the real and imaginary axes. In the complex plane, any rotation in 2D space can be represented.

With this, we can represent all rotations in 2D space. A useful formula for this is the Euler’s formula.

Euler’s formula is useful for representing a number with magnitude $r$ and an angle $\theta$ from the x-axis.

\[re^{i\theta} = r(\cos\theta + i\sin\theta)\]

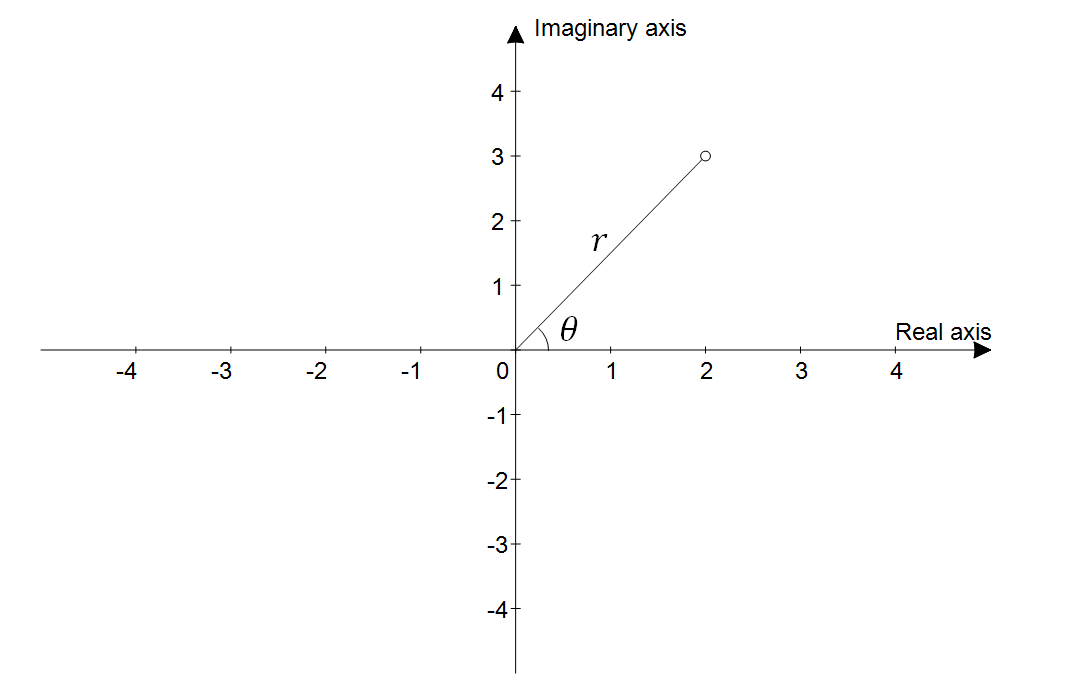
Figure 5. Euler's formula makes it convenient to represent complex numbers using magnitude and direction.

Returning to negative numbers, using the complex plane and Euler’s formula, we can represent -1 as shown in Figure 6, with a magnitude of 1 and an angle of $\pi$ radians (180 degrees) from the real axis.

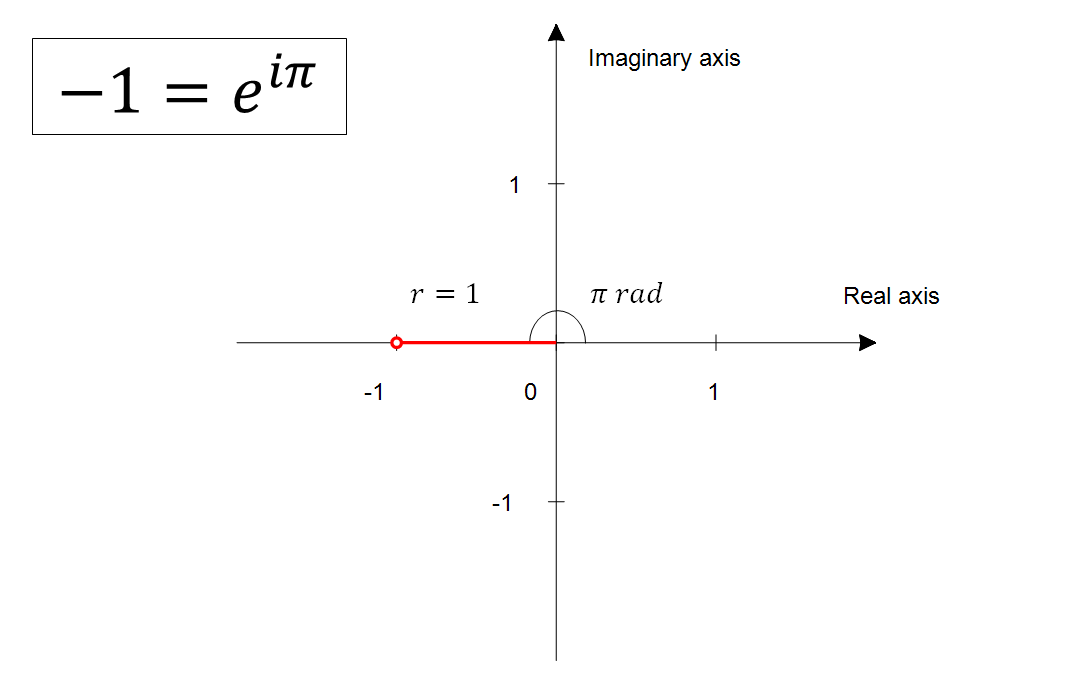
Figure 6. In the complex plane, -1 is a number with magnitude 1 and an angle of 180 degrees (pi radians) from the real axis.

Exponential Functions with Negative Base

What is $(-1)^x$? (where $x$ is a real number)

Using Euler’s formula, $-1$ can be expressed as $e^{i\pi}$, so $(-1)^x$ can be written as follows:

\[(-1)^x = (e^{i\pi})^x = e^{ix\pi}\]

When interpreting equation 3, using Euler’s formula, we can say that $(-1)^x$ represents the position of a point on the $x$-axis with an angle of $x\pi$ radians.

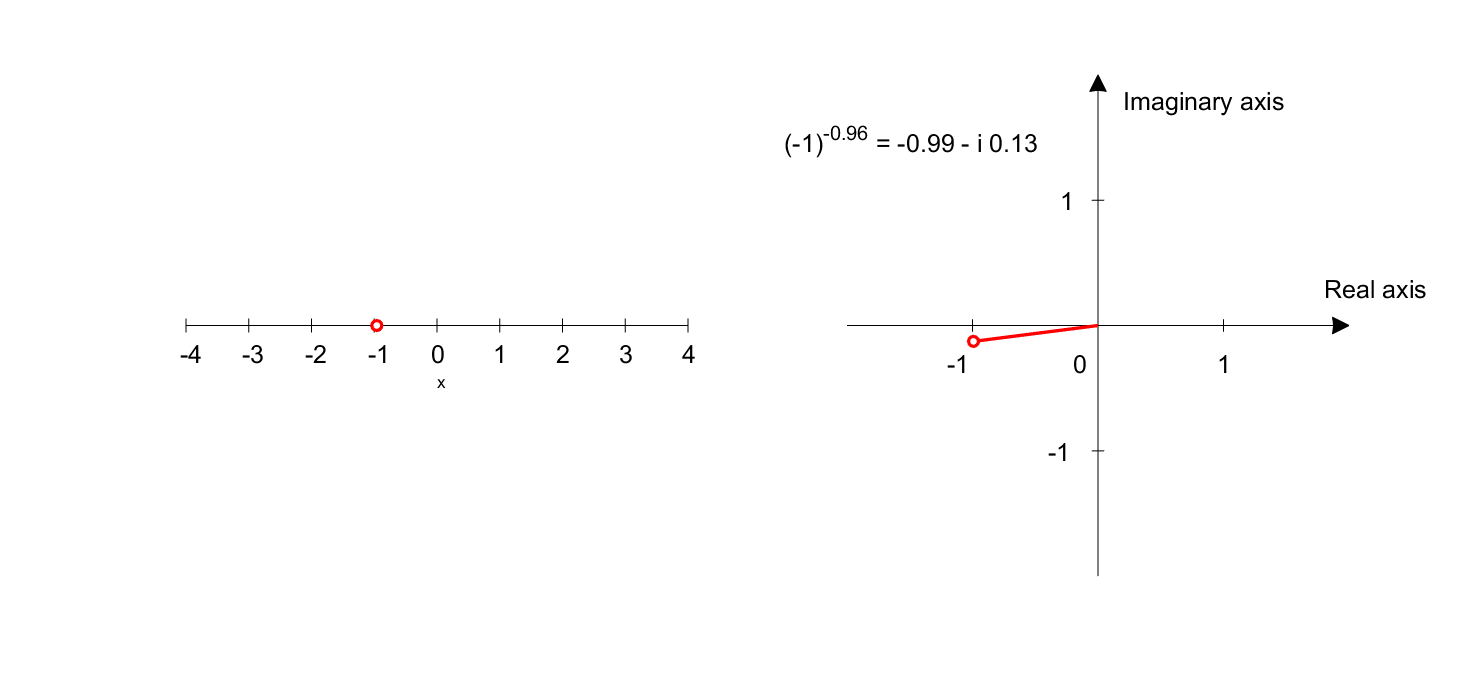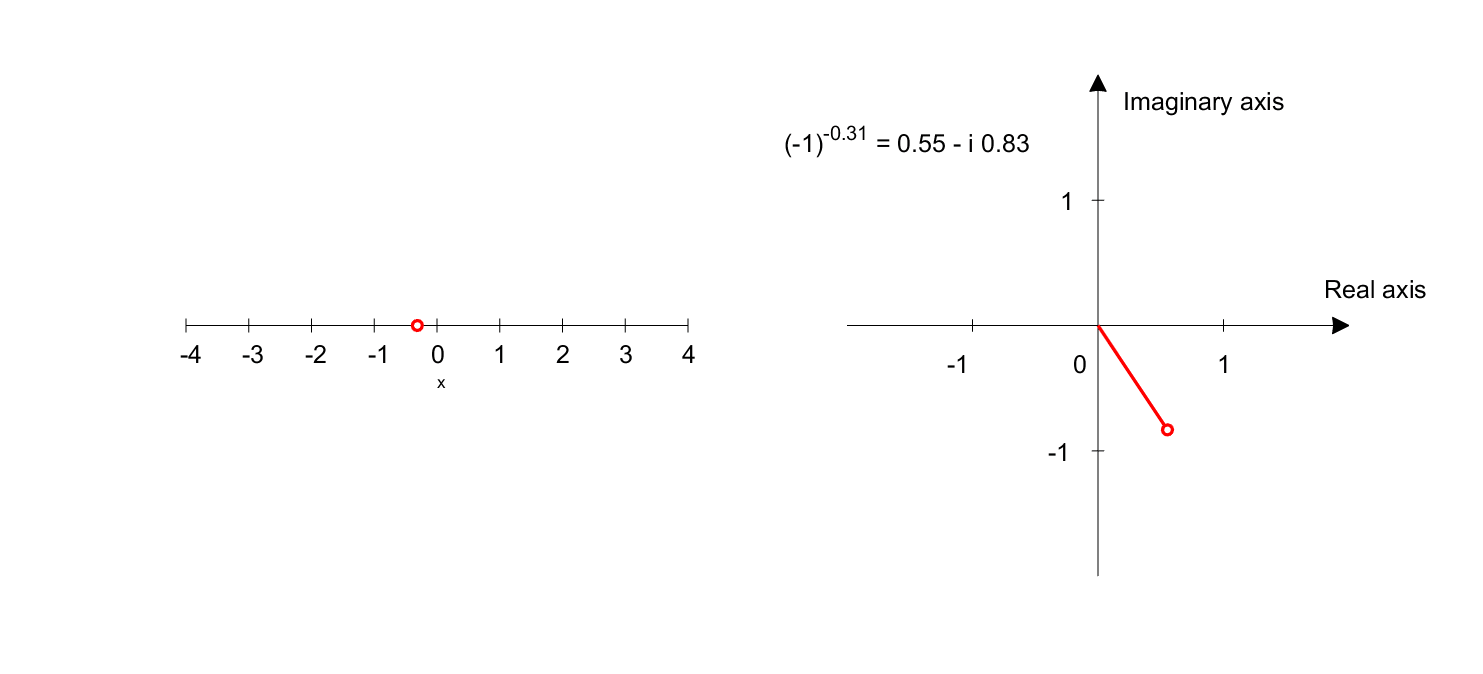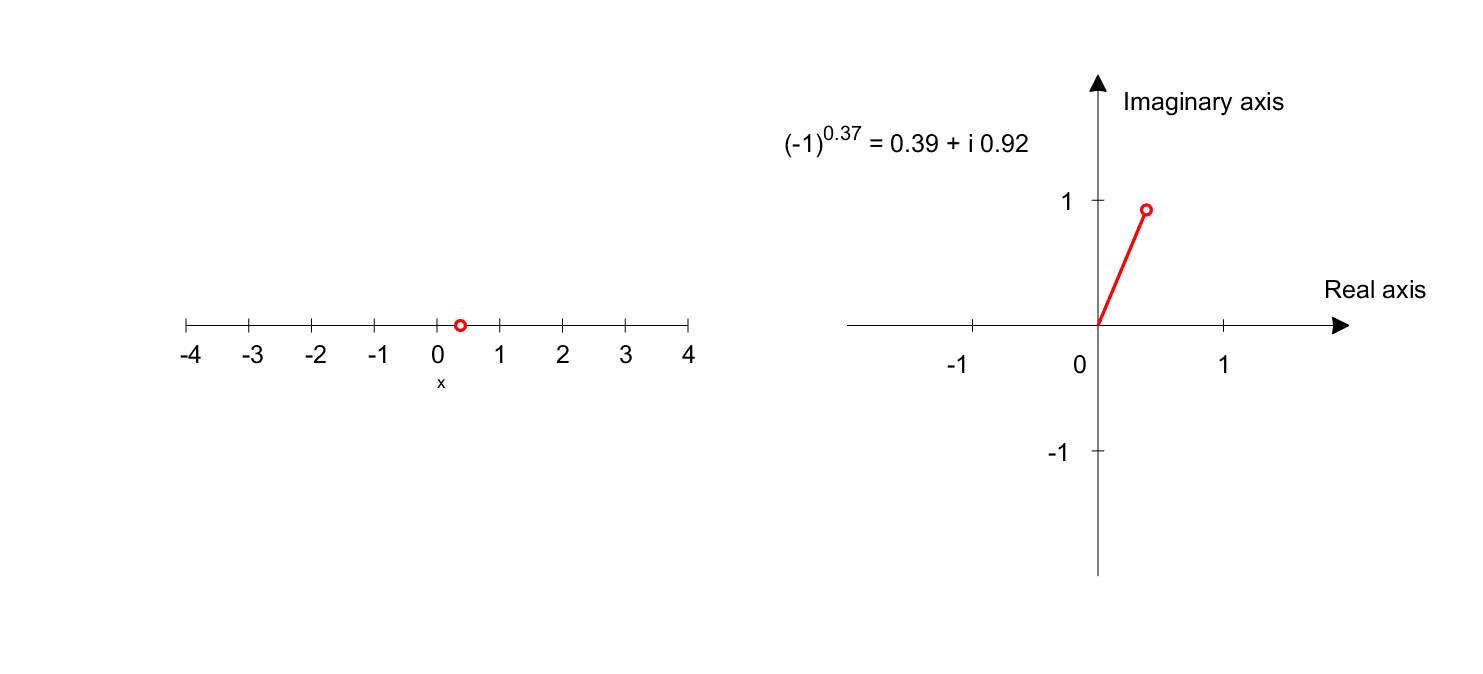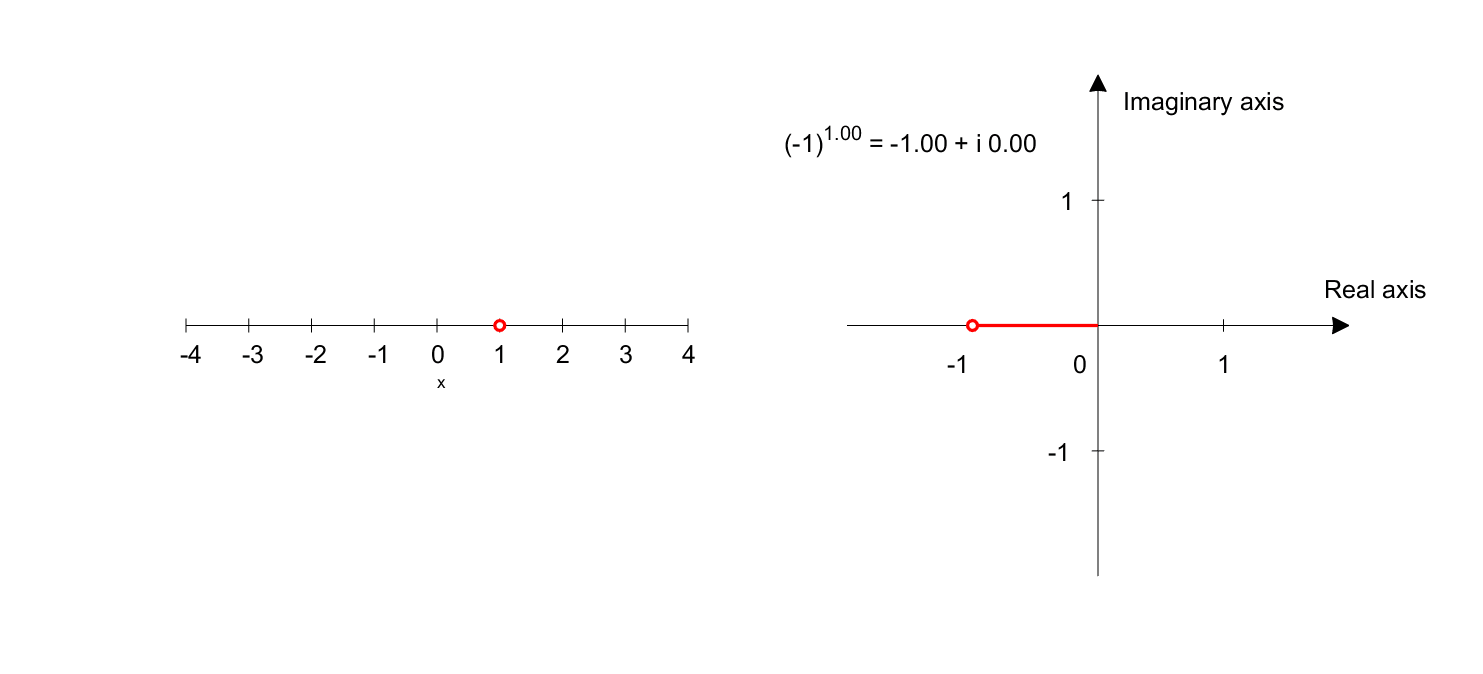
Figure 7. Graph representing $(-1)^x$. The left plot shows the domain, and the right plot shows the range.

What is $(-1.5)^x$? (where $x$ is a real number)

Using a similar method, what if the base is not -1 but -1.5?

\[(-1.5)^x = (1.5 \times (-1))^x = (1.5 \times e^{i\pi})^x = 1.5^x \times e^{ix\pi}\]

Looking closely at equation 4, we can see that $1.5^x$ increases in value as $x$ gets larger, and $e^{ix\pi}$ rotates as seen in equation 3 and Figure 7, depending on the magnitude of $x$.

Therefore, the result of equation 4 will show that the value increases and rotates as $x$ gets larger.

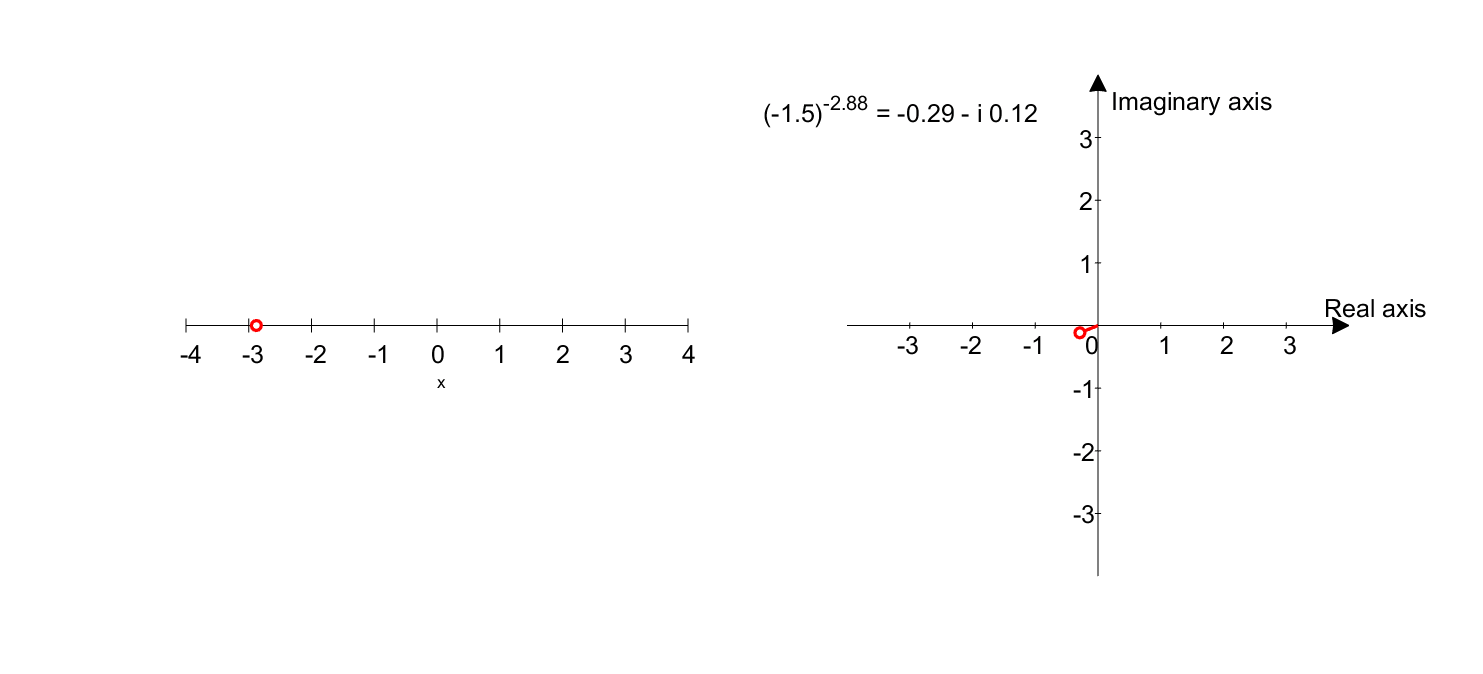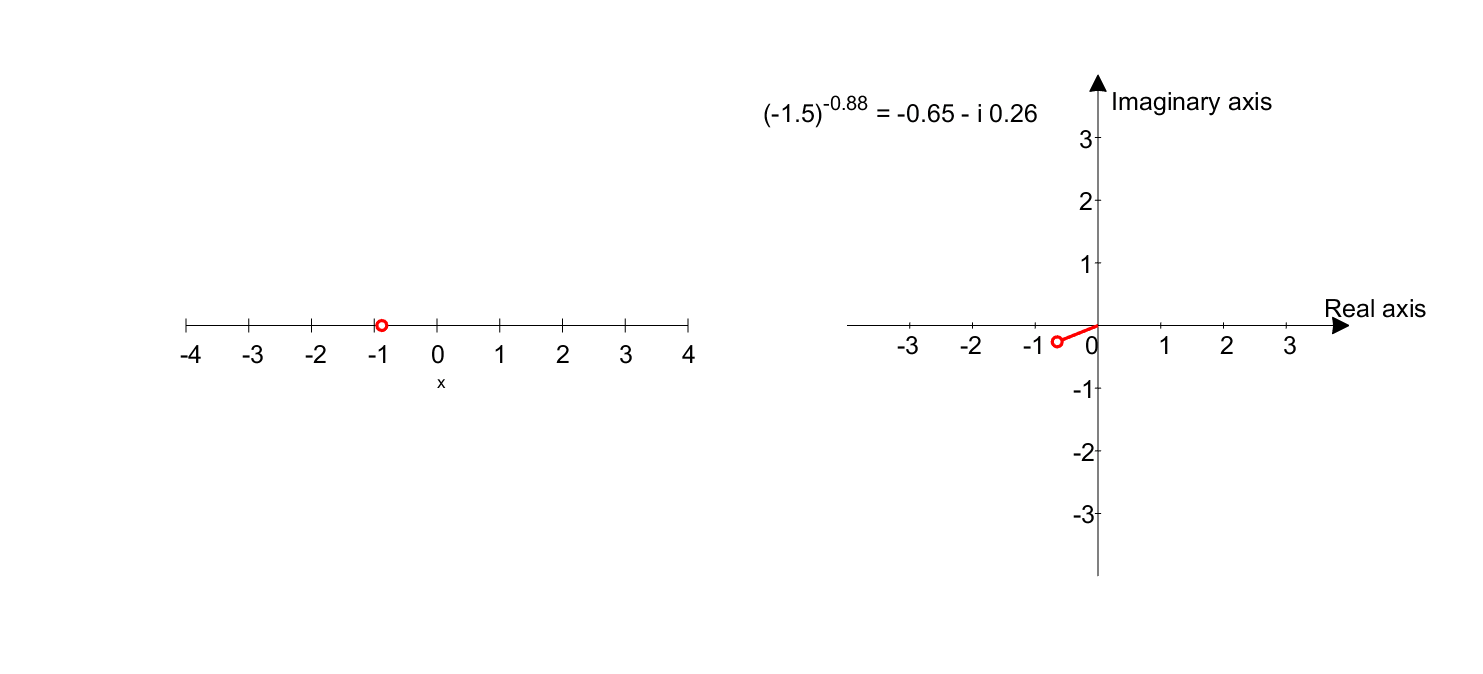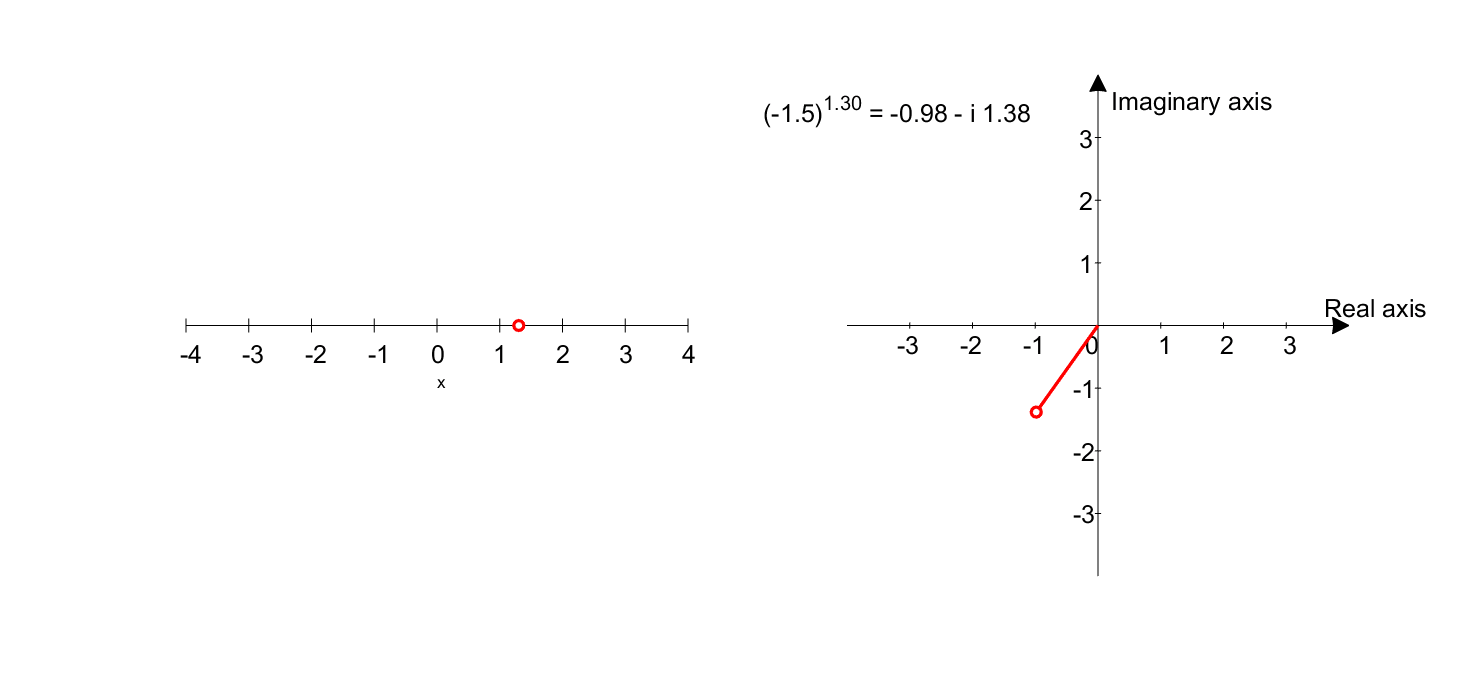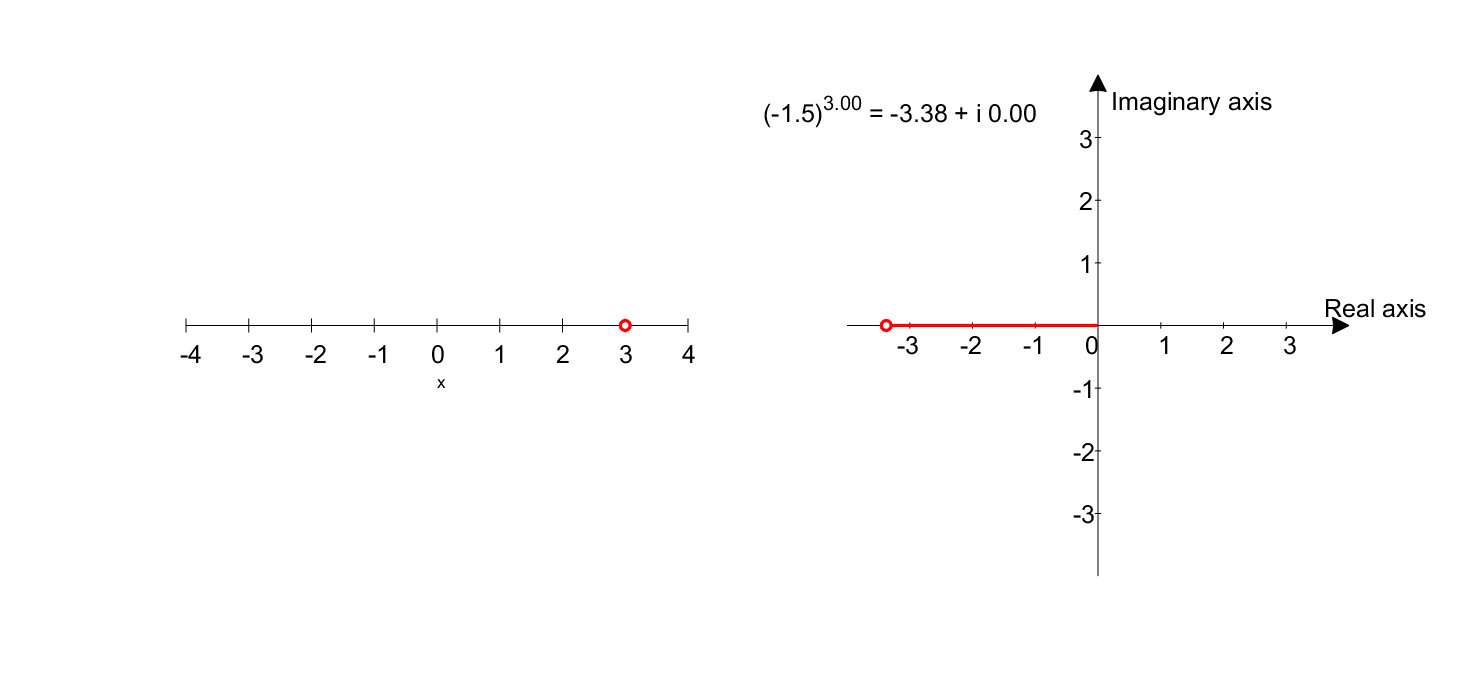
Figure 8. Graph representing $(-1.5)^x$. The left plot shows the domain, and the right plot shows the range.

If we represent the flow over time with colors, we can obtain the same graph as the beginning of this article, as shown in Figure 9.

Figure 9. Graph representing $(-1.5)^x$ with colors indicating the flow over time.

Another way of visualization

So far, we have visualized the exponential function with negative base by separating the domain and range. However, there is another way to visualize it where we can display the domain and range at once.

However, in this method, we need to draw the real and imaginary parts of the range separately.

For instance, the graph of $y=(-1.5)^x$ is shown in Figure 10 below.

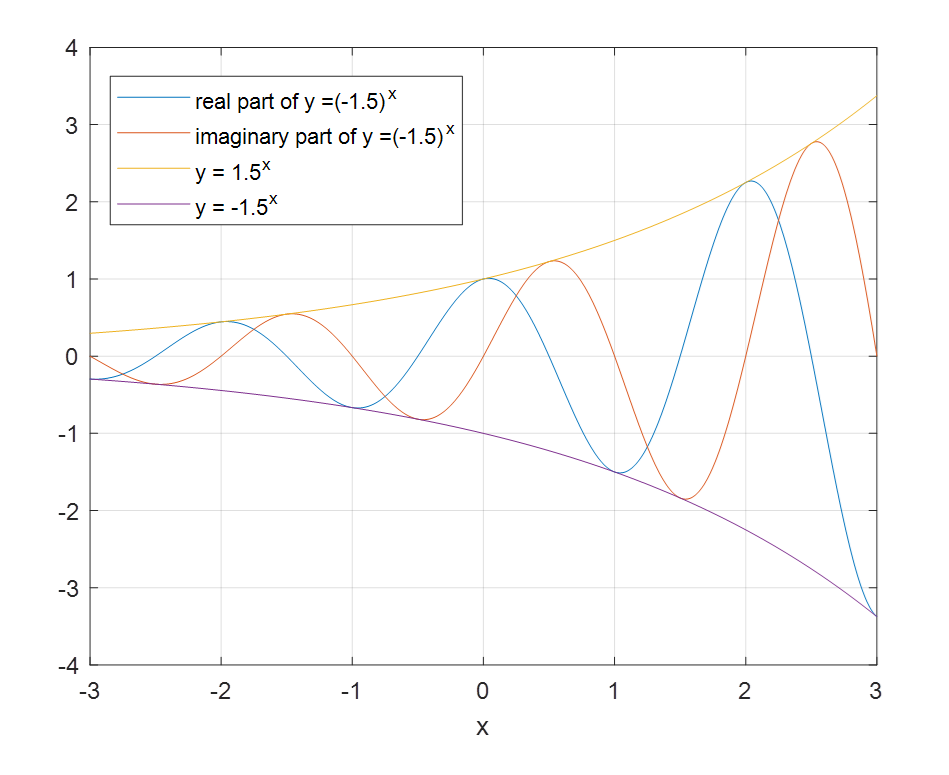
Figure 10. Visualization of the exponential function with negative base that can display the domain and range at once.