Meaning of Multiple Integral

The meaning of multiple integrals. Let's break down the volume under the function into smaller parts and add them up.
※ Using only the values of the lower part of the function surface, the estimated volume is smaller than the integral value.

Starting from the concept of definite integrals

The concept of multiple integrals can be understood in various ways, but let’s start from the content related to the calculation of area/volume, which is the most visually understandable.

During high school, you may have learned the concept of definite integrals using the method of Riemann sums.

Figure 1 shows the process of using Riemann sums to calculate the area under a function curve.

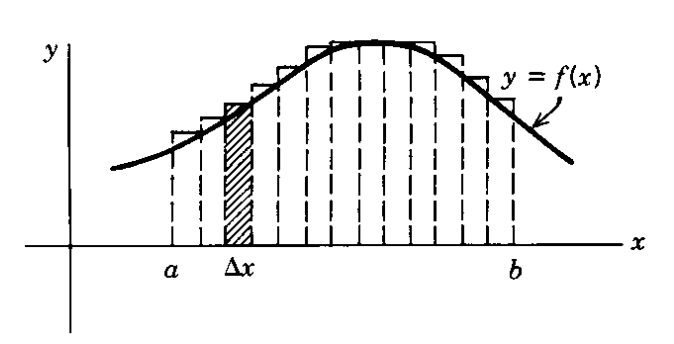
Figure 1. Obtaining the concept of definite integrals through the process of using Riemann sums to calculate the area under the function curve.
Figure source: Fig 2.1 on p.242 of Boas' "Mathematical Methods in the Physical Sciences" textbook

If the function is given as $y = f(x)$, then we consider the area of small rectangles by multiplying by the length of $\Delta x$, and add them up from $a$ to $b$.

In mathematical notation, we can express the estimated value of the area using Riemann sums as follows:

\[\sum_{x=a}^{b}f(x)\Delta x\]

By taking the limit as $\Delta x$ approaches 0 and summing up the areas of infinitely many rectangles obtained by making the base length of the rectangles very small, we can calculate the area under the curve more closely to the true value, as shown in the following equation:

\[\Rightarrow \lim_{\Delta x \rightarrow 0}\sum_{x=a}^{b}f(x)\Delta x=\int_{a}^{b}f(x)dx\]

Here, using the fundamental theorem of calculus, we can calculate the integral value in equation (2) as follows, since

\[\frac{d}{dx}F(x) = f(x)\]

where $F(x)$ is an antiderivative of $f(x)$ and is known.

\[Equation(2) = F(b) - F(a)\]

Extension of the concept of definite integrals to multiple integrals

Let’s extend the concept of definite integrals to multiple integrals by generalizing the concept of definite integrals.

Using the method of partitioning, we can calculate the volume under a two-dimensional surface.

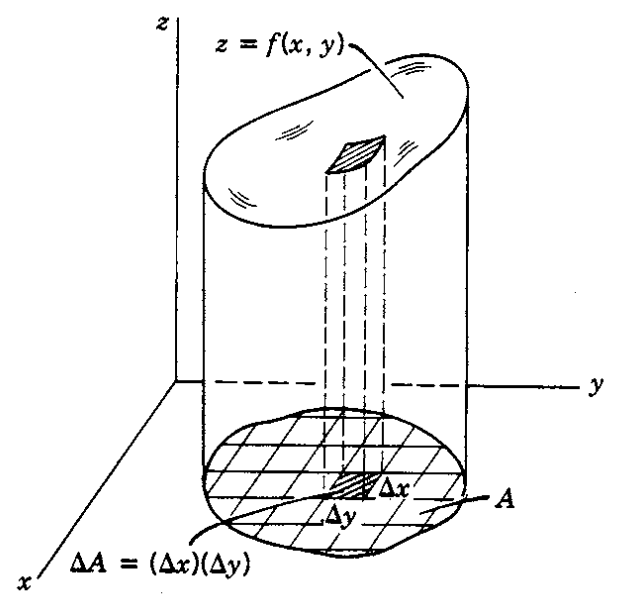
Figure 2. Using the method of partitioning, we can find the volume under the function f(x, y).
Figure source: Boas' Mathematical Methods in the Physical Sciences, p. 242, Fig. 2.2.

In Figure 2, we see a cylindrical object with a circular base lying on a three-dimensional Cartesian coordinate space, with a height given by the function $z=f(x,y)$.

Comparing Figure 1 and Figure 2, we can observe several differences between definite integrals and multiple integrals. First, in definite integrals, the infinitesimal length given by $\Delta x$ is replaced by $\Delta A = \Delta x \Delta y$ in multiple integrals.

Also, the concept of the “area of a small square” in definite integrals, $f(x)\Delta x$, is extended to the concept of the “volume of a small wooden stick” in multiple integrals, which is given by $f(x,y)\Delta x \Delta y$.

The comparison between definite and multiple integrals can be summarized in the following table:

Table 1. Comparison of the concepts of definite and multiple integrals.

Just as we added up the areas of small squares in definite integrals, we will add up the volumes of small wooden sticks in multiple integrals.

The height of a cube can be calculated as the product of its base and height. In this case, the height is given by $f(x,y)$ and the area of the base is given by $\Delta x \Delta y$, so we can consider the volume of a small wooden stick as follows:

\[f(x,y)\Delta x\Delta y\]

Then, just as we added up the areas of small squares from $a$ to $b$ in definite integrals, in multiple integrals we will add up the volumes of small wooden sticks for appropriate values of $x$ and $y$.

\[\sum_x\sum_y f(x,y)\Delta x \Delta y\]

Finally, just as we used the concept of limits in definite integrals, we can use the same concept to converge the volume value as follows:

\[\lim_{\Delta x \rightarrow 0}\lim_{\Delta y \rightarrow 0}\sum_x\sum_y f(x,y)\Delta x \Delta y = \iint_Af(x,y)dxdy\]

What are the appropriate ranges for x and y in a double integral?

In figure 1, in a definite integral, x changes from $a$ to $b$.

However, as seen in figure 2, when the shape of the base is not simple, how should we determine the ranges of x and y in a double integral?

\[\iint_Af(x,y)dxdy = \int_{x=?}^{?}\int_{y=?}^{?}f(x,y)dxdy\]

Let’s consider projecting the base of the solid, as shown in figure 3, onto the x-axis. Let’s call the values determined at the two ends as $x=a$ and $x=b$ respectively.

Also, let’s divide the edge of the base along a horizontal line parallel to the x-axis into two halves, and name one side as $y_1(x)$ and the other side as $y_2(x)$.

Let’s try to understand the description in words by referring to the diagram below.

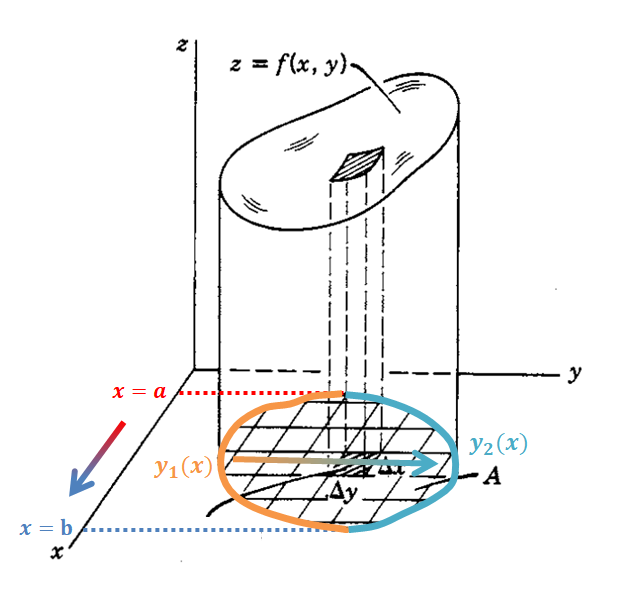
Figure 3. Method for determining the ranges of x and y for an arbitrary-shaped base on the xy-plane
Image source: Fig 2.2 on p.242 of Boas' "Mathematical Methods in the Physical Sciences"

In a definite integral, we calculated the sum by changing x from $a$ to $b$.

In a double integral, x accumulates from $a$ to $b$, and y accumulates from $y_1(x)$ to $y_2(x)$, as we can think from the expression (8) above, we can determine the integration ranges for x and y in the double integral as follows:

\[\iint_Af(x,y)dxdy = \int_{x=a}^{b}\int_{y=y_1(x)}^{y_2(x)}f(x,y)dxdy\]

If we further analyze the equation, we can see that the expression for y is entirely determined as a function of x, so it ultimately becomes an integration with respect to x, just like calculating a definite integral, allowing us to solve the double integral.

Example of a Double Integral Problem

Now, let’s solve an example problem to actually calculate a double integral.

Let’s calculate the volume of a solid enclosed by the plane $z=1+y$, the xz-plane, the yz-plane, and the plane $2x+y=2$, as shown in figure 4.

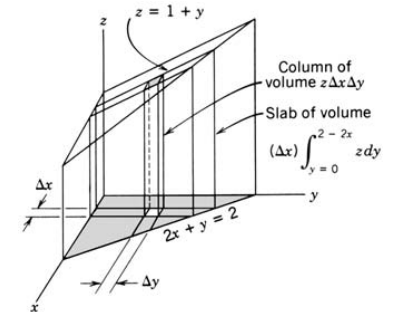
Figure 4. Example of a double integral calculation
Image source: Fig 2.3 on p.243 of Boas' "Mathematical Methods in the Physical Sciences"

As explained above using the method of double integration, the double integral value can be expressed in a single equation as follows:

\[\iint_A z dydx = \iint_A (1+y)dy dx\]

Here, the notation $A$ under the double integration symbol represents the triangular region shaded in gray in Figure 4, indicating that the double integration should be performed with respect to this region as the base.

In Figure 4, the base of the triangular region is formed by the plane $2x+y=2$ in the $x, y$ coordinate system. Therefore, we can say that the range of $x$ is $[0, 1]$ and when stacking in the $y$ direction, the minimum value of $y$ is $y=0$, and the maximum value is $y=2-2x$.

Therefore, Equation (10) can be written as follows:

\[\int_{x=0}^{x=1}\int_{y=0}^{y=2-2x}{(1+y)dydx}\]

Expanding the inner integral with respect to $y$ first, we get:

\[\Rightarrow \int_{x=0}^{x=1}\left|y+\frac{1}{2}y^2\right|_{y=0}^{y=2-2x}dx\] \[=\int_{x=0}^{x=1}2-2x+\frac{1}{2}(2-2x)^2dx\] \[=\int_{x=0}^{x=1}4-6x+2x^2dx\]

Now, let’s calculate the definite integral value with respect to $x$.

\[\Rightarrow \left|4x-3x^2+\frac{2}{3}x^3\right|_{0}^{1}\] \[=4-3+\frac{2}{3} =\frac{5}{3}\]

Thus, the volume of the solid object we want to find is $\frac{5}{3}$, which can be calculated through double integration.