Let’s consider an arbitrary complex number $x+iy$.
Here, let’s assume that $x$ and $y$ are real numbers.
This value can also be expressed using polar coordinates as follows:
If the distance from the origin to $x,y$ is $r$ and the angle between the $x$-axis and the point is $\theta$, then
\[x+iy = r\cos(\theta) + i r\sin(\theta)\]
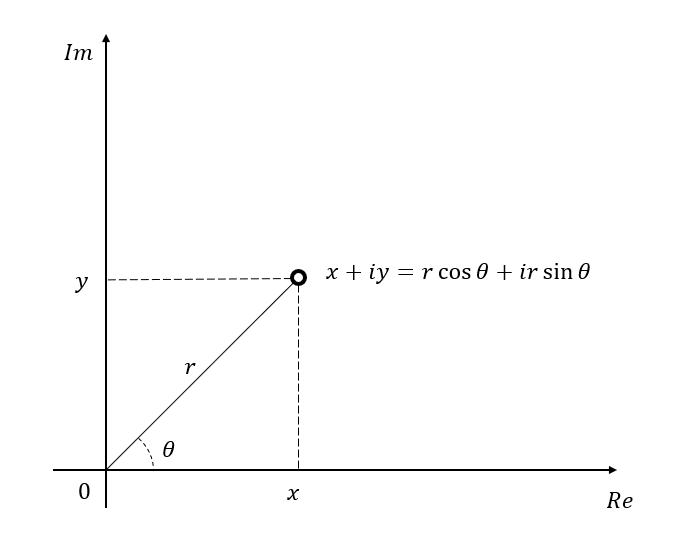
Figure 1. A point on the complex plane represents a complex number.
Let’s assume $r=1$ and call this value $z$.
\[z = \cos(\theta) + i \sin(\theta)\]This value $z$ represents a point on the unit circle with a radius of 1.
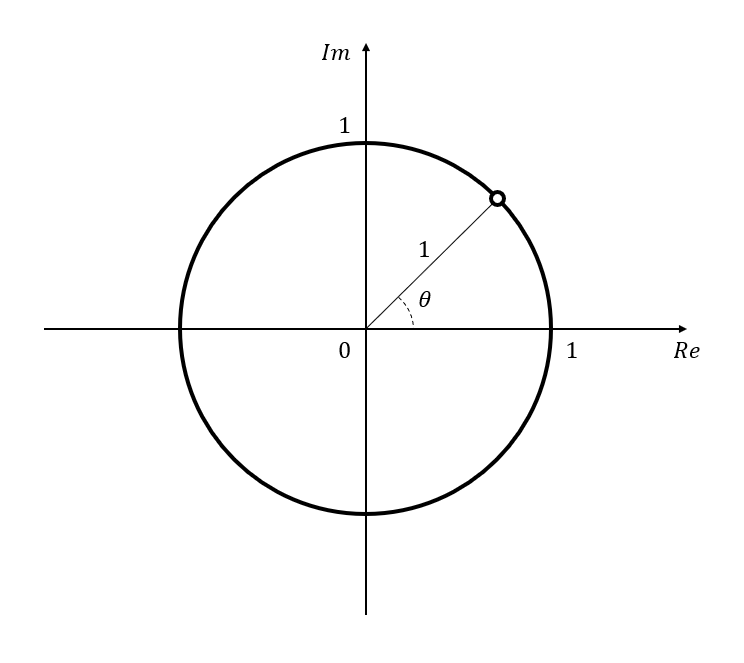
Figure 2. The point $z$ on the unit circle on the complex plane. The angle between $z$ and the $x$-axis is $\theta$.
Now, let’s differentiate $z$ with respect to $\theta$. The value is as follows:
\[\frac{dz}{d\theta}=-\sin(\theta) + i \cos(\theta)\]Let’s multiply both sides by $-i$.
So, we can see that
\[(-i)\frac{dz}{d\theta} = (-i)(-1)\sin(\theta) + (-i)(i)\cos(\theta)\] \[=\cos(\theta) + i\sin(\theta)\]However, Equation (5) is the same as Equation (2), so we can conclude that
\[(-i)\frac{dz}{d\theta}=z\]Now let’s rearrange Equation (6) slightly so that all the expressions involving $z$ are on the left-hand side and all the expressions involving $\theta$ are on the right-hand side:
\[Equation\ (6) \Rightarrow \frac{dz}{z}=\frac{1}{(-i)}d\theta\] \[\Rightarrow \frac{dz}{z}=id\theta\]Now we can integrate both sides of Equation (8):
\[\int\frac{dz}{z}=\int i d\theta\] \[\Rightarrow \ln(z)=i\theta + C\]Here, $C$ is the constant of integration.
We can rewrite this equation as follows:
\[z = A_0 e^{i\theta}\]where $A_0$ is an arbitrary constant.
Now, let’s determine the value of $A_0$. Since equation (11) is the same as equation (2), we can write:
\[A_0e^{i\theta}=\cos(\theta) + i \sin(\theta)\]Considering the case where $\theta=0$, we get:
\[A_0 = \cos(0)+i\sin(0) = 1\]Therefore,
\[e^{i\theta}=\cos(\theta) + i \sin(\theta)\]as desired.