Let's explore the shape of the geometric distribution for various values of parameter p by modifying it.
What does k on the x-axis represent in the geometric distribution?
Can you explain what the shape of the geometric distribution represents?
Prerequisites
To understand the geometric distribution, it is recommended to know the following:
Definition of the Geometric Distribution
The geometric distribution is a distribution of the number of attempts $k$ it takes to obtain the first success in a sequence of independent trials with two possible outcomes (success or failure), where the probability of success in each trial is $p$.
The probability of obtaining the first success on the $k$th trial is given by
\[P(K=k) = (1-p)^{k-1}p\]where $k = 1, 2, 3, \cdots$.
If we look closely, the sequence of probability values $P(K=k)$ is a geometric sequence, where each term is continuously multiplied by $(1-p)$, which means it is a geometric distribution.
Shape of the Geometric Distribution
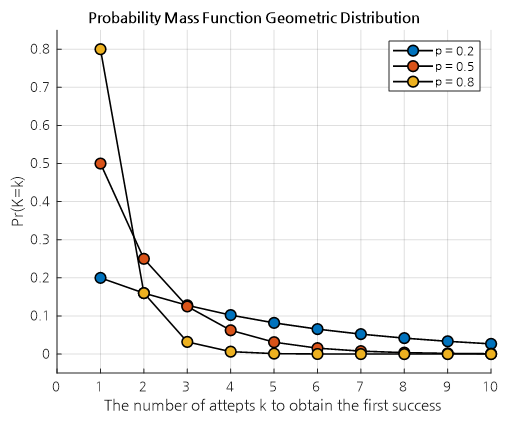
Figure 1. The shape of the geometric distribution for various values of p.
What is shown in the geometric distribution is the probability of achieving the first success on the k-th attempt when the success probability is $p$.
For example, in the case of p = 0.8 shown in Figure 1, the probability of succeeding on the first attempt is 0.8, and the probability of succeeding on the second attempt is 0.2 * 0.8 = 0.16 since one failure must occur before success.
Also, the probability of succeeding on the third attempt is 0.2 * 0.2 * 0.8 = 0.032.
What we can understand from this is that as the value of $p$ increases, the probability of success at $k=1$ also naturally increases.
One comforting point is that if $p$ is not large, it is possible to achieve the first success with a higher probability after multiple attempts than when $p$ is large.
Geometric Distribution Problem Solving
There are many problems that can be understood through geometric distribution, and since the formula itself is not complex, it may not be difficult to solve problems.
Problem 1.
Suppose you keep rolling a die until a 1 comes up. Calculate the probability that a 1 appears on the sixth roll.
Problem 1 Solution
The probability of a 1 appearing on a die is 1/6, so the probability of a 1 appearing on the sixth roll is the same as a 1 not appearing five times in a row and a 1 appearing on the sixth roll.
Therefore,
\[\Rightarrow (5/6)^5\times (1/6)^1=0.06698\]which is approximately 6.7%.
Problem 2.
There is an exam known for its extremely low pass rate. The pass rate for this exam is 20%. What is the probability that a person will pass the exam within three tries?
Problem 2 Solution
In this problem, we can calculate the probability of passing on the first try + the probability of passing on the second try + the probability of passing on the third try.
Therefore,
\[\Rightarrow (0.2) + (0.8)\times(0.2) + (0.8)^2\times(0.2) = 0.448\]In other words, there is a 44.8% chance of passing within three attempts.