Transformation from s-plane to z-plane
Move the slider to see the changes :D

Laplace Transform and Z-transform

※ This post is taken from the Z-transform and Laplace Transform post of Z Transform.

Z-transform can be thought of as the discrete time version of Laplace Transform.

Let’s obtain the Z-transform by performing time sampling on the Laplace Transform equation.

For a continuous-time signal $x(t)$, Laplace Transform is defined as follows:

\[\mathfrak{L}\left[x(t)\right] = X(s) = \int_{0^{-}}^{\infty}x(t) e^{-st}dt\]

To time-sample the continuous-time signal $x(t)$, we substitute $t\rightarrow nT$ for a sampling period $T$. Thus,

\[X(s) = \int_{0^{-}}^{\infty}x(t) e^{-st}dt \big |_{t\rightarrow nT}\]

and $x(nT)$ can be viewed as a discrete time signal. Therefore,

\[X(z) = \sum_{n=0}^{\infty}x(nT)e^{-snT}\]

If we substitute $z=e^{sT}$, then

\[Formula (3) \Rightarrow \sum_{n=0}^{\infty}x[n]z^{-n}\]

Through this derivation, we can confirm that Laplace and Z-transform are mathematically related. In conclusion, Laplace Transform and Z-transform can be seen as techniques to examine the characteristics of a system, with the difference lying in the way they define complex numbers.

The s-plane and z-plane have the following morphological relationship.

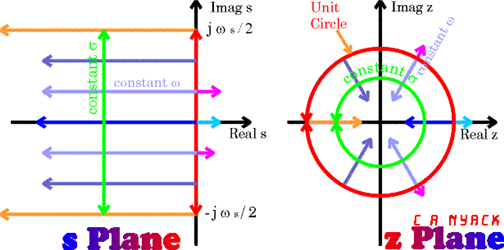
Figure 1. Relationship between s-plane and z-plane. The z-plane appears to be a folded version of the s-plane.

As shown in Figure 1, in the s-plane, poles should be located to the left of the vertical axis to have a stable system, while in the z-plane, poles should be located inside the unit circle to have a stable system.