Definition of the natural number $e$
First, let’s take a look at the definition and value of the natural number $e$.
| DEFINITION 1. natural number $e$ |
|---|
$$e = \lim_{n\rightarrow \infty}\left(1+\frac{1}{n}\right)^n$$ Alternatively, the approximate value of $e$ expressed as a decimal is as follows: $$e = 2.71828 18284 59045 23536 \cdots$$ |
The natural number $e$ may seem unnatural when considered purely as a number, but there must be a reason why such a constant was introduced.
Just like the value of pi ($\pi$) may seem meaningless as a number, such as 3.14159 265359 …, it actually has significance in calculating the circumference, area, and other properties of a circle. Similarly, the natural number $e$ is expected to have some meaning.
Significance of the natural number $e$
The natural number $e$ can be regarded as a constant designed to represent the continuous growth of nature.
More specifically, it represents the amount of growth obtained when experiencing one continuous growth with a 100% growth rate.
In the above statement, the two words in bold are the key points.
Meaning of growing continuously once with a 100% growth rate
Let’s imagine a magical piggy bank. Suppose this piggy bank increases by exactly 1 dollar after 1 year when you put in 1 dollar (i.e., a 100% growth rate). We can assume that this has grown once.
This can be represented graphically as follows:
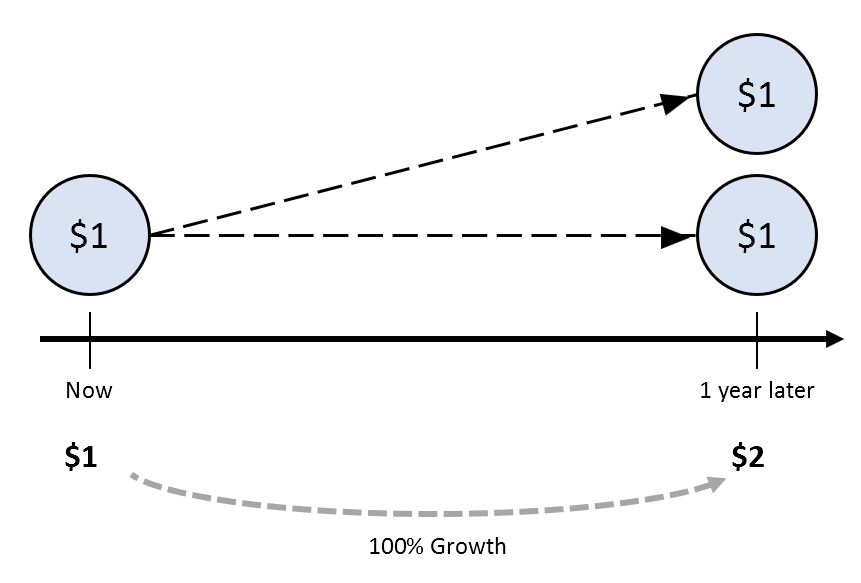
Figure 1. Magical piggy bank that grows by 100% after 1 year
Now, what if we change the setting to grow by 50% every 6 months?
After 6 months, 1 dollar becomes 0.5 dollars, and after another 6 months, that 0.5 dollars becomes… Describing it in words would be complicated, so let’s represent it graphically as shown in Figure 2 below.
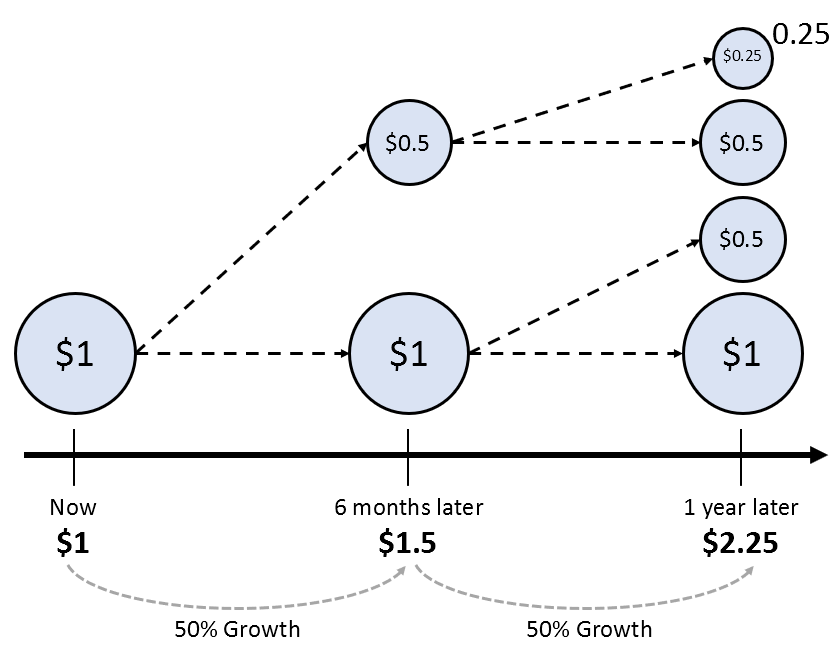
Figure 2. The magic piggy bank that grows by 50% every 6 months
The key point here is that if you grow it by 50% every 6 months as shown in Figure 2, it will become 2.25 dollars instead of 2 dollars after one year.
That is, it has increased by 0.25 dollars more than if it had grown by 100% all at once as in Figure 1.
Now, let’s see what happens if we divide it into 3 parts and grow it.
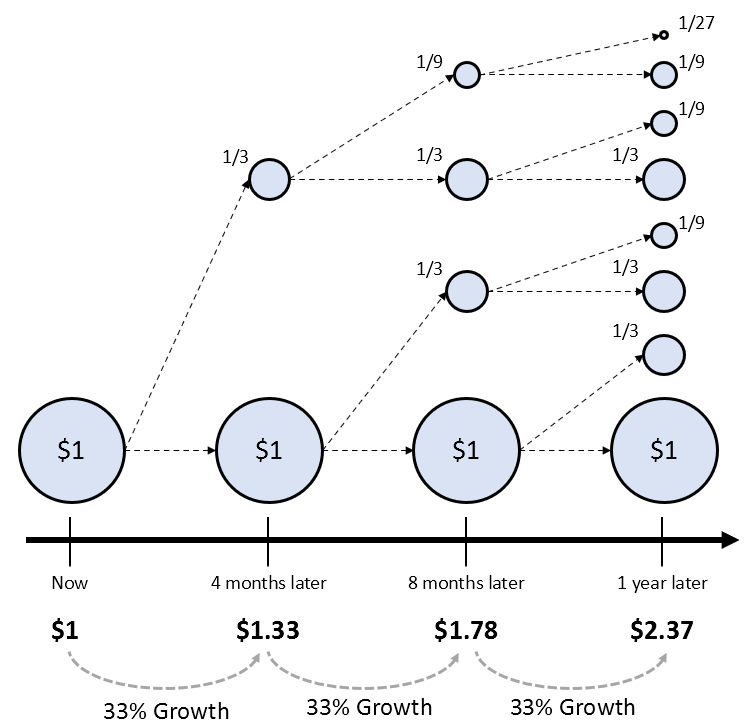
Figure 3. The magic piggy bank that grows by 33.33% every 4 months
As expected, growing by 33.33% every 4 months produces more growth than growing by 50% every 6 months.
Naturally, you may wonder:
“What happens if we divide it infinitely? Will the growth rate also increase infinitely?”
To answer this question, we need to formulate the contents of Figures 1, 2, and 3 into equations.
The formula for Figure 1 is as follows:
\[1+1 = 2\]The formula for Figure 2 is as follows:
\[(1+0.5)\times (1+0.5)\]We can explain why Figure 2 can be written as equation (4) as follows:
If we expand the equation (4), we get:
\[Equation(4) = 1\times(1+0.5) + 0.5\times(1+0.5)\]That is, the original 1 dollar in Figure 2 becomes 1.5 dollars in the first term on the right-hand side, and the 0.5 dollars obtained after 6 months becomes 0.75 dollars in the second term.
Using the same principle, we can formulate Figure 3 into an equation as follows:
\[(1+\frac{1}{3})^3\]Using the same principle, we can achieve the following results by dividing 100% growth into n times and promoting growth.
\[(1+\frac{1}{n})^n\]Then, if we infinitely divide, we can think of the growth rate with the following formula.
\[\lim_{n\rightarrow \infty}(1+\frac{1}{n})^n\]As we know, equation (8) is a number defined as the natural constant $e$, and its value is approximately 2.718.
The concept of infinitely dividing and promoting growth can be understood in relation to the previously mentioned “continuous growth.”
Regarding Growth Frequency and Growth Rate
As mentioned earlier, the natural constant $e$ represents the growth rate obtained when growing by 100% growth rate in 1 continuous growth. Furthermore, it was noted that with a 100% growth rate, the growth rate would be $e$ when growing continuously once.
Then, what would happen if we have a 50% growth rate and grow continuously once?
In mathematical notation, it would be as follows:
\[\lim_{n\rightarrow \infty}\left(1+\frac{50\%}{n}\right)^n\] \[=\lim_{n\rightarrow \infty}\left(1+\frac{1}{2n}\right)^n\] \[=\lim_{n\rightarrow \infty}\left(1+\frac{1}{2n}\right)^{2n/2}\] \[=e^{1/2}\]Also, if we have a 100% growth rate and grow continuously twice, the growth rate would be
\[e\times e = e^2\]In other words, the meaning of the exponent $x$ in the equation $e^x$ is
\[e^{\text{Number of Growth Times x Growth Rate}}\]Meaning of Natural Logarithm
As mentioned earlier, the meaning of the exponent $x$ in the equation $e^x$ is related to multiplying the number of growth times and the growth rate.
Mathematically, this implies one of the meanings of natural logarithm can be deduced easily.
That is, it is a mathematical technique that allows us to reverse calculate the product of the number of growth times and the growth rate when we know a certain growth rate.
In other words, if we know the growth amount denoted as A, and we can express it as $A = e^{\text{number of growths} \times \text{growth rate}}$ using the natural logarithm, we can calculate the number of growths multiplied by the growth rate as follows:
\[\ln(e^{\text{number of growths} \times \text{growth rate}}) = \text{number of growths} \times \text{growth rate}\]Differentiation of Exponential Functions with Natural Base
In high school calculus, we learn about the differentiation of exponential functions with the natural base $e$.
The most important point in this context is that the derivative of an exponential function with base $e$ is itself the exponential function.
In other words,
\[\frac{d}{dx}e^x = e^x\]Just like how using radians instead of degrees makes the differentiation of trigonometric functions cleaner, using $e$ as the base for differentiation of exponential functions also results in a cleaner derivative.
But what if the base is a positive real number other than $e$? How would the result change?
The formula is as follows:
\[\frac{d}{dx}a^x = a^x \ln(a)\]That’s why in calculus, we often consider as many exponential functions as possible to have $e$ as the base.
Now, let’s revisit the differentiation of exponential functions with the natural base, which was our original concern.
How should we interpret the meaning of Equation (16)?
There are two points to consider:
-
Does Equation (16) really represent continuous growth?
-
Does the base of the exponential function in Equation (16) have to be $e$?
Let’s replace $y=e^x$ in Equation (16) with an arbitrary function $y$. Then we see a differential equation.
\[\frac{dy}{dx}=y\]“What does Equation (18) mean? Why is it related to growth?
To understand this, let’s rewrite the original formula of differentiation.
Let’s assume $y=f(x)$.
\[Equation (18) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=f(x)\]Although we wrote it down to this extent, the limit in Equation (19) seems difficult, so let’s start by considering the case when $h=1$.
1. Does Equation (16) really mean exponential growth?
1) Case when $h=1$
To think more deeply about the meaning of Equation (16), let’s bring Equation (19) and gradually make the value of $h$ smaller.
\[Equation (19)\Rightarrow \frac{f(x+1)-f(x)}{1} = f(x)\] \[\Rightarrow f(x+1) = 2f(x)\]What does Equation (21) mean? It means $f(x) = 2^x$. If we draw a graph, it looks like the following:
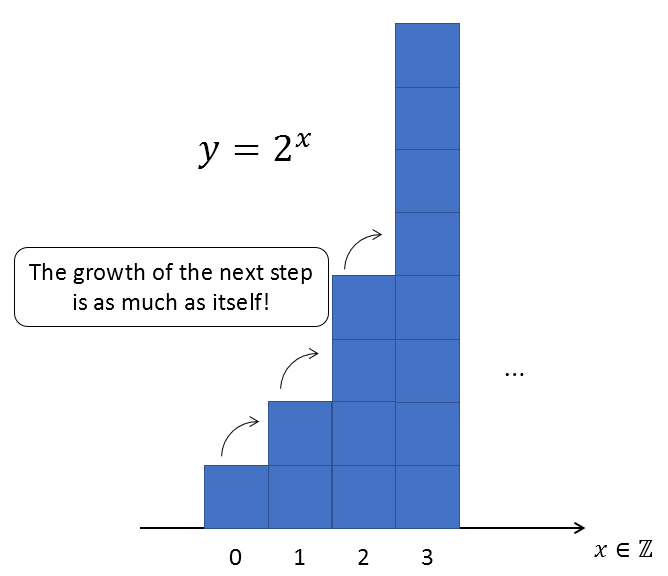
Figure 4. The growth rate of $f=2^x$ at every $x$ is itself.
In other words, we can see the meaning of Equation (18) in more detail when $h=1$. It means the rate of change is itself.
In other words, it means that the function grows by the current size of the function at the next $x$.”
2) When $h=0.5$
Let’s now consider the case where $h=0.5$ in equation (19).
\[\text{Equation (19)} \Rightarrow \frac{f(x+0.5)-f(x)}{0.5}=f(x)\] \[\Rightarrow f(x+0.5) = 1.5 f(x)\]In this way, we can also think about cases where $h$ is very small.
3) When $h=0.00001$
\[\text{Equation (19)} \Rightarrow \frac{f(x+0.00001)- f(x)}{0.00001}=f(x)\] \[\Rightarrow f(x+0.00001) = 1.00001f(x)\]What does equation (25) mean? It means that,
In other words, it means that we will increase the function value by a very small amount at each step, which is continuous growth.
2. Should the base of the exponential function in equation (16) be $e$?
Let’s rewrite equation (18).
\[\frac{dy}{dx}=y \notag\]To solve the differential equation of equation (18), we move all $y$ terms to the left-hand side and all $x$ terms to the right-hand side, which gives us the following.
\[\Rightarrow \frac{1}{y}dy = dx\]Now, let’s integrate both sides.
\[\Rightarrow \int \frac{1}{y}dy = \int dx\]Here, the definition of $\ln(y)$ is exactly $\int\frac{1}{y}dy$, so the value on the left-hand side is equivalent to $\ln(y)$.
This can be verified by showing that the derivative of $\ln(x)$ is $1/x$, as shown below.
In other words,
\[\frac{d}{dx}\ln(x) = \frac{1}{x}\]Therefore, by the fundamental theorem of calculus,
\[\int \frac{1}{x}dx = \ln(x)+C\] \[\text{where }C\text{ is the constant of integration}\notag\]To see why this is true,
\[\frac{d}{dx}\ln(x) = \lim_{h\rightarrow 0}\frac{\ln(x+h)-\ln(x)}{h}\] \[=\lim_{h\rightarrow 0}\frac{\ln\left(\frac{x+h}{x}\right)}{h}\] \[=\lim_{h\rightarrow 0}\ln\left(\frac{x+h}{x}\right)^{\frac{1}{h}}\] \[=\lim_{h\rightarrow 0}\ln\left(1+\frac{h}{x}\right)^{\frac{x}{h}\cdot\frac{1}{x}}\] \[=\ln(e^{\frac{1}{x}})=\frac{1}{x}\]Therefore, we can write equation (27) as follows:
\[\Rightarrow \ln(y) = x\]So,
\[y=e^x\]In other words, the function in equation (18) is an exponential function with a base of $e$.