What are the conditions for a matrix to be positive definite?
Prerequisites
To better understand positive definite matrices, it is recommended that you have knowledge about the following topics.
- Matrix and Linear Transformation
- Eigenvalues and Eigenvectors
- Geometric Interpretation of Hessian Matrix
Definition
First, let’s take a closer look at the definition of a positive definite matrix.
A matrix $A$ is positive definite if for any nonzero column vector $x$ and symmetric matrix $A$, the following inequality holds.
\[x^TAx >0\]This definition may seem strange at first glance. Why do we take the transpose of one side of the column vector $x$ and not the other side when defining a matrix?
Meaning of Positive Definite Matrices
The Meaning of the Name “Positive Definite”
“Positive definite” is related to signs. In other words, if a matrix is positive definite, it implies that the way positive numbers work applies in a similar way.
Let’s consider an arbitrary positive real number $a$. Also, let’s consider an arbitrary real number $b$.
If $a$ is positive, then it is a very basic result that multiplying $b$ by $a$ maintains its sign.
In other words, if $a$ is positive, then multiplying $b$ by $a$ increases the magnitude of $b$ but does not reverse its direction.
Now let’s consider arbitrary vectors $a$ and $b$. Let’s also think about the inner product of these two vectors. The inner product that is generally defined is calculated as follows.
\[a^Tb = |a||b|\cos(\theta)\]Here, $\theta$ is the angle between $a$ and $b$. And when the condition $-\pi/2 \lt \theta \lt \pi/2$ is satisfied, $a^Tb > 0$.
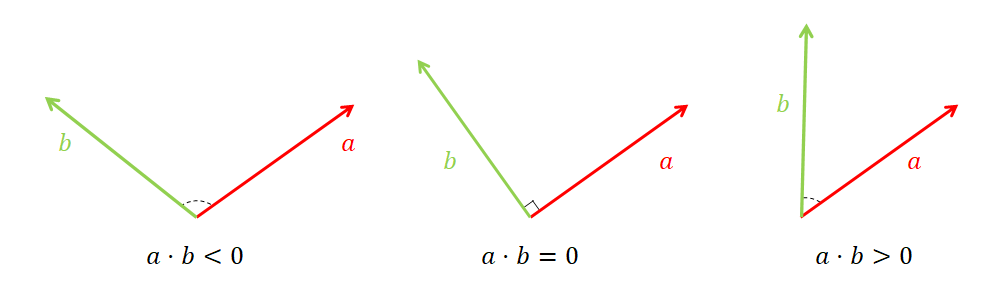
Figure 1. When the angle between the two vectors is acute, the inner product is positive; when it is obtuse, the inner product is negative.
Now, if we think about the definition of a positive definite matrix, an arbitrary symmetric matrix $A$ is a positive definite matrix if it satisfies the following condition for any nonzero column vector $x$.
\[x^TAx>0\]Let’s rewrite $x^TAx$ using parentheses as follows.
\[x^TAx \rightarrow x^T(Ax)\]That is, the above equation can also be interpreted as taking a linear transformation $A$ of an arbitrary nonzero vector $x$, and then taking the inner product with the original $x$.
As mentioned earlier, for two vectors to have a positive inner product, the angle between the two vectors must satisfy $-\pi/2 \lt \theta \lt \pi/2$.
Therefore, when we apply a linear transformation to x, we can interpret it as a change in angle between -90 degrees and 90 degrees before and after the transformation.
In other words, when using a positive definite matrix, such as a positive real number, the linear transformation must not ‘flip’ the input vector.
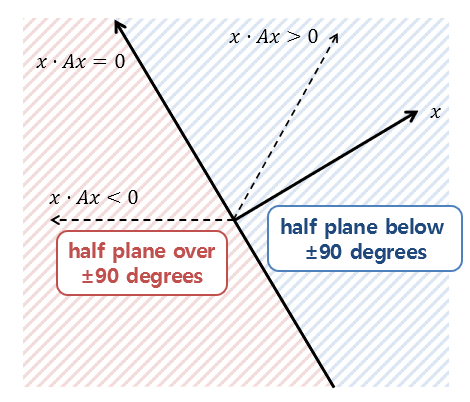
Figure 2. A positive definite matrix ensures that the change in angle before and after the transformation is between -90 and 90 degrees (i.e., it keeps the vector within the blue region even after transformation).
Positive Definite Matrix and Eigenvalues
Although the properties of a positive definite matrix are defined based on its definition, the signs of its eigenvalues are closely related to it.
\[Ax=\lambda x\] \[x^TAx = x^T\lambda x=\lambda |x|^2\]Since $x^TAx > 0$ by definition, $\lambda>0$.
In other words, under the condition that matrix A is a symmetric matrix, the condition that all eigenvalues are positive is a condition that A is a positive definite matrix.
However, if we reconsider the meaning of eigenvalues, they indicate the directionality of linear transformations performed by the matrix.
Eigenvalues indicate how much a matrix changes in the direction of its eigenvectors, and the fact that the eigenvalues are positive means that the transformation scales up or down in that direction, but does not flip it.
Let’s use the Javascript Applet at the top of this post to think more about this.
By clicking on the circle at the end of the red arrow, we can select the desired matrix A by determining the basis vectors after linear transformation.
If the red arrow and the green arrow do not flip within -90 degrees to 90 degrees of each other, matrix A is a positive definite matrix, whereas if the red arrow and the green arrow move beyond -90 to 90 degrees or if the two arrows are flipped, it is not a positive definite matrix.
Meanwhile, we can also check the changes in eigenvalues. If the matrix is positive definite, meaning that arrows do not flip or there is a change of only -90 degrees to 90 degrees, then all eigenvalues are positive. If not, we can see that at least one of the two eigenvalues will be negative.
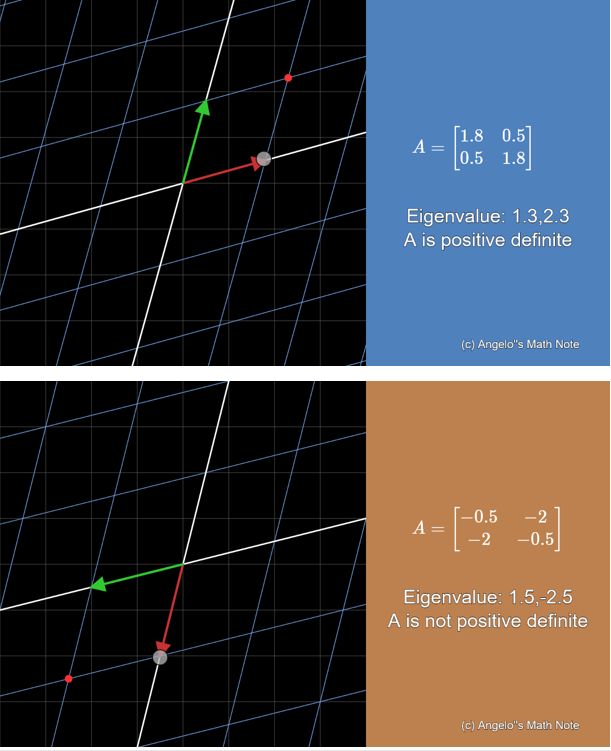
Figure 3. At least one of the two eigenvalues becomes negative when the base vectors are flipped or the angle between them exceeds -90 to 90 degrees after linear transformation.
Positive Definite and Hessian Matrix
One of the most important applications of positive definite matrices is in the field of optimization.
In optimization theory, finding the minimum value of a function is one of the ultimate goals.
In a previous post about the Hessian matrix, it was mentioned that the Hessian matrix has a similar meaning to the second derivative.
In a sense, the Hessian matrix performs a geometric transformation that makes the basic bowl shape more convex or concave, as shown in the following figure:
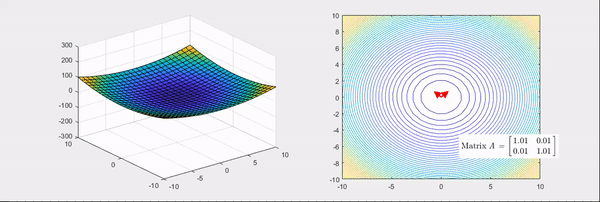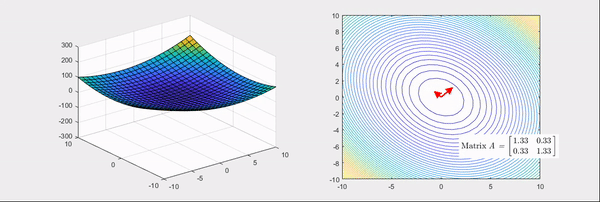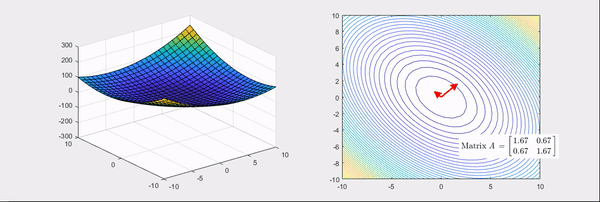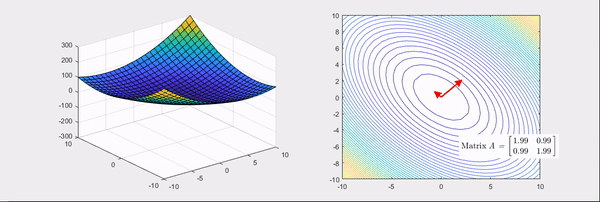
Figure 4. When all eigenvalues of the Hessian matrix are positive.
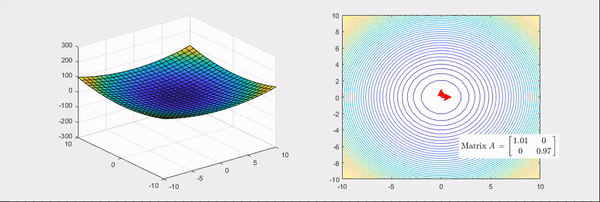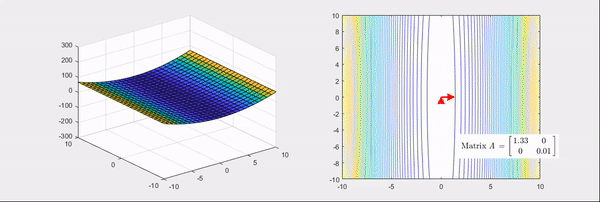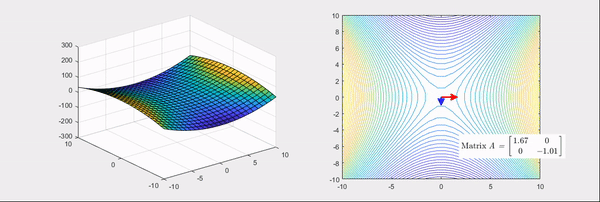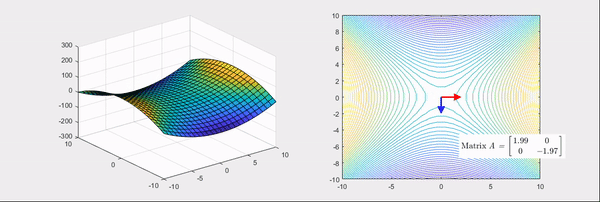
Figure 5. When one of the eigenvalues of the Hessian matrix is positive and the other is negative.
The arrows in the above pictures represent the directions of the eigenvectors of the Hessian matrix, where the red color indicates the case when the eigenvalues are positive and the blue color indicates the case when the eigenvalues are negative.
As can be seen, when all eigenvalues of the Hessian matrix are positive, the linear transformation using the Hessian matrix results in a more convex basic bowl shape.
On the other hand, as shown in the second picture, when one of the eigenvalues is positive and the other is negative, the basic bowl shape changes into a saddle shape.
In other words, the Hessian matrix is a symmetric matrix, and when all eigenvalues of the Hessian matrix are positive, it means that the Hessian matrix is a positive definite matrix.
In other words, if the Hessian matrix of any twice differentiable real function f is positive definite, the overall shape of the function is convex downwards, and inevitably has a local minimum.
If we find the point where the gradient is zero by calculating the gradient here, we can know that the point is the local minimum.