Derivation of Taylor Series Formula

The formula for Taylor series can be derived from the fundamental theorem of calculus in calculus.

The fundamental theorem of calculus can be written as follows:

\[\int_{a}^{x}{f'(t)dt} = f(x) - f(a)\]

We can slightly modify the left-hand side of equation (1) as follows:

\[\int_{a}^{x}{1\cdot f'(t)dt} = f(x) - f(a)\]

Here, we want to perform partial integration on the left-hand side of equation (2).

Let’s set $u’=1$ and $v = f’(t)$.

Then, we have:

\[u = t, \space v' = f''(t)\]

Note that although we usually set $u=t$, in fact, $u$ should be written as $u=t+C$, where $C$ is the constant of integration. Here, let’s set $C$ as $-x$ for convenience.

Since the variable of integration is $t$, $x$ is just a constant.

Therefore, instead of equation (4), let’s consider $u$ and $v’$ as follows:

\[u = t-x, \space v' = f''(t)\]

Then, equation (2) can be expanded as follows:

\[\Rightarrow (t-x)f'(t)\big|^{x}_{a}-\int_{a}^{x}(t-x)f''(t)dt\]

In the first term of equation (6), when we substitute $t=x$, the value becomes 0, and when we substitute $t=a$, the value becomes $(a-x)f’(a)$. Since we are subtracting this term, the equation can be written as follows:

\[\Rightarrow (x-a)f'(a) - \int_{a}^{x}(t-x)f''(t)dt\]

Continuing to expand equation (7), we have:

\[\Rightarrow (x-a)f'(a) - \left\{ \frac{1}{2}(t-x)^2f''(x)\big|_{a}^{x} - \int_{a}^{x}\frac{1}{2}(t-x)^2f'''(t)dt \right\}\]

As in equation (6), when we substitute $t=x$ into the second term of equation (8), the value becomes 0, and when we substitute $t=a$, the value becomes $1/2 \times (a-x)^2f’‘(a)$. Now it’s time to subtract it. Therefore, by continuing to expand equation (8), we have the following:

\[\Rightarrow (x-a)f'(a) + \frac{1}{2}(x-a)^2f''(a) + \frac{1}{2}\int_{a}^{x}(t-x)^2f'''(t) dt\]

By continuing the expansion in the same way,

\[\Rightarrow (x-a)f'(a) + \frac{1}{2}(x-a)^2f''(a) + \frac{1}{2}\cdot\frac{1}{3}(t-x)^3f^{(3)}(t)\big|_{a}^{x}-\int_{a}^{x}\frac{1}{2}\cdot\frac{1}{3}(t-x)^3f^{(4)}(t)dt\]

Continuing to add in this manner, we can see that the following pattern emerges¹.

\[\Rightarrow \sum_{n=1}^{\infty}\frac{1}{n!}(x-a)^nf^{(n)}(a)\]

Since the original equation (11) is derived from equation (1), we have:

\[f(x)-f(a) = \sum_{n=1}^{\infty}\frac{1}{n!}(x-a)^nf^{(n)}(a)\]

Rearranging equation (12), we get:

\[f(x) = f(a) + \sum_{n=1}^{\infty}\frac{1}{n!}(x-a)^nf^{(n)}(a)\] \[\Rightarrow f(x) = \sum_{n=0}^{\infty}\frac{1}{n!}(x-a)^nf^{(n)}(a)\]

Characteristics and Meaning of Taylor Series

Approximation using Polynomial Functions

Looking at the formula of Taylor series in equation (14), we can see that Taylor series can represent any function as a polynomial function.

This property is very useful when approximating transcendental functions. For example, when approximating $y=e^x$ at the point $x=0$, we have:

\[e^x = \sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots\]

Approximation at a Single Point

One of the characteristics of Taylor series is that it approximates the function values around a specific point.

If we plot the approximation of $y=e^x$ at $x=0$ using MATLAB, we get the following graph:

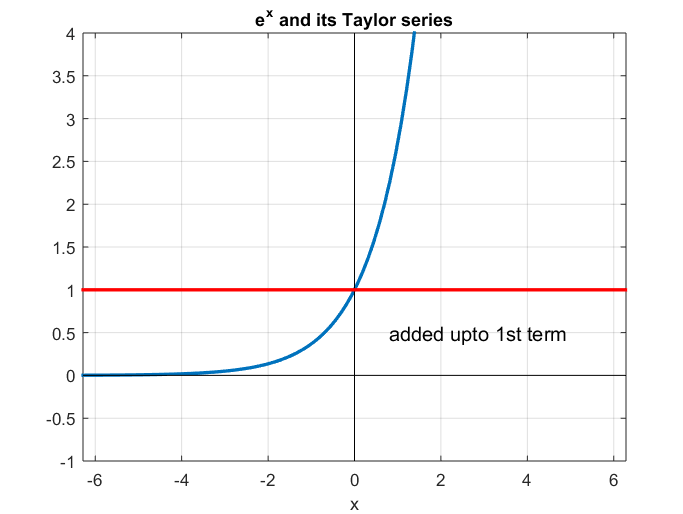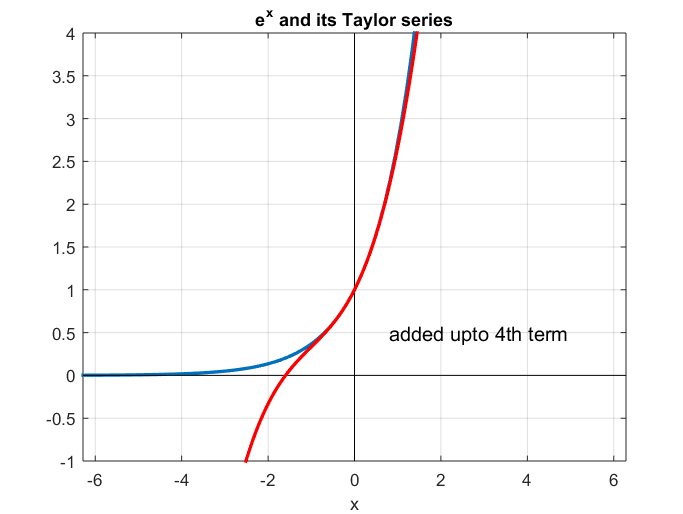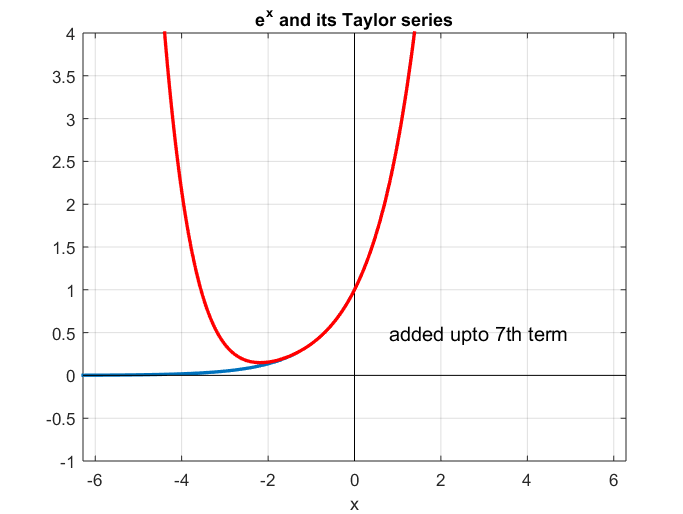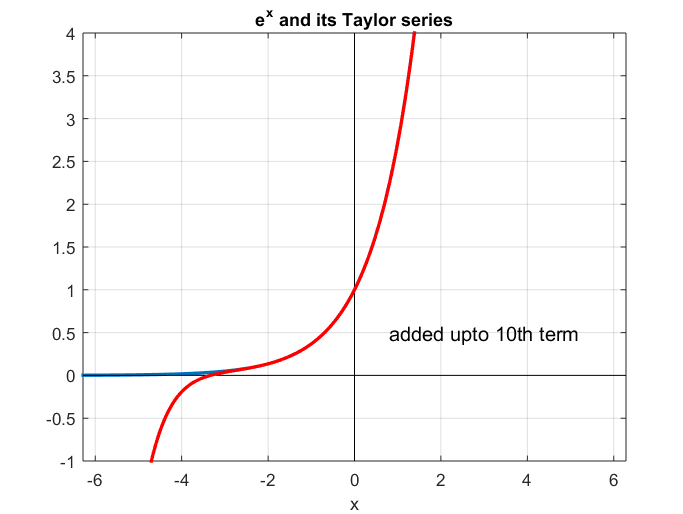
Figure 1. Approximation of y=exp(x) at x=0 using Taylor series

In addition, Taylor series can also be applied to multivariate functions. Figure 2 shows an approximation at the point (1,1) for a function with two independent variables. As more terms are added, we can see that the approximation becomes closer to the shape of the original function.

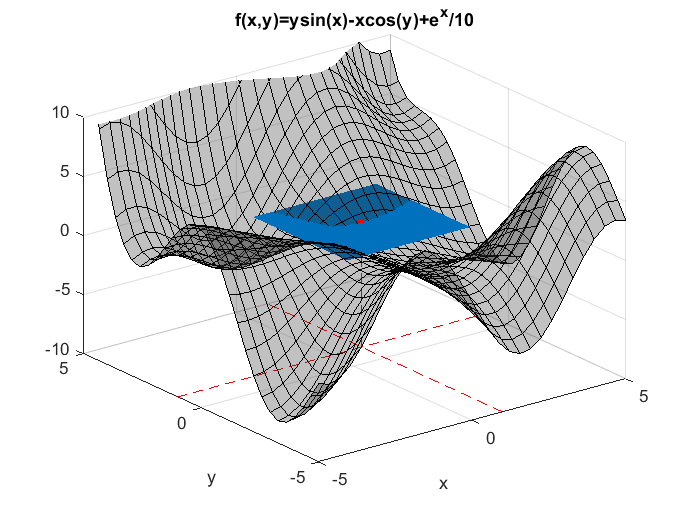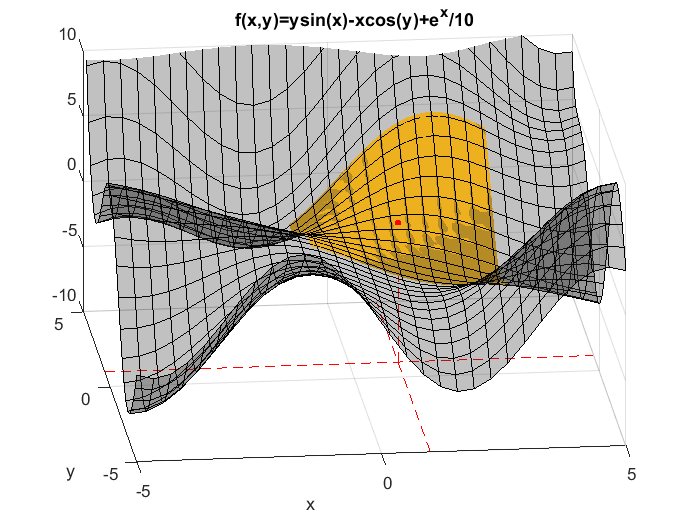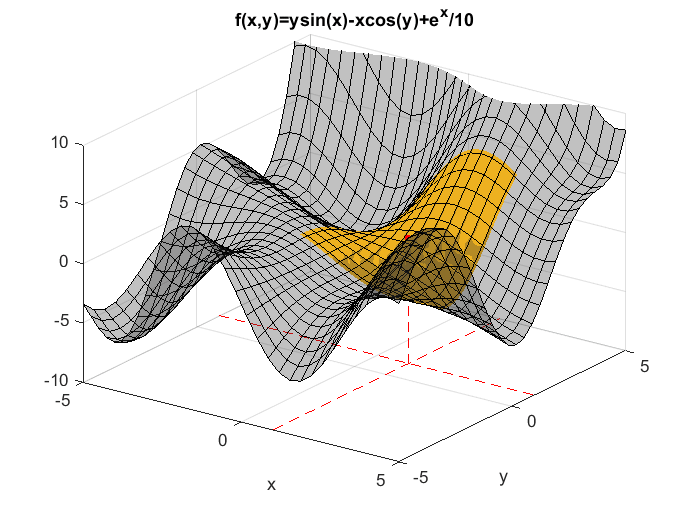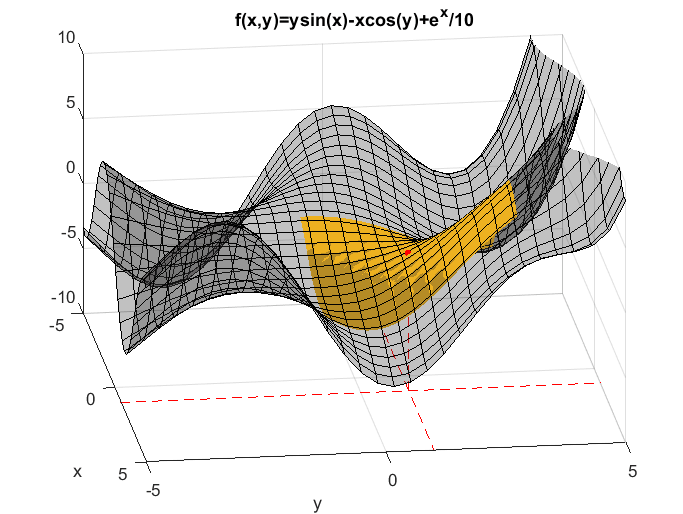
Figure 2. Approximation of a multivariate function at (1,1)

Figures 1 and 2 illustrate the characteristic of Taylor series, which approximates a function near a specific point.

On the other hand, Fourier series is a contrasting series, which approximates a function within a specific interval, rather than at a specific point.

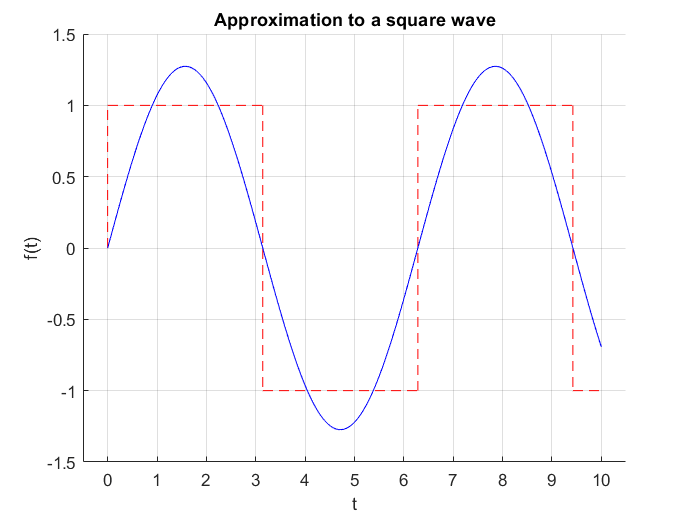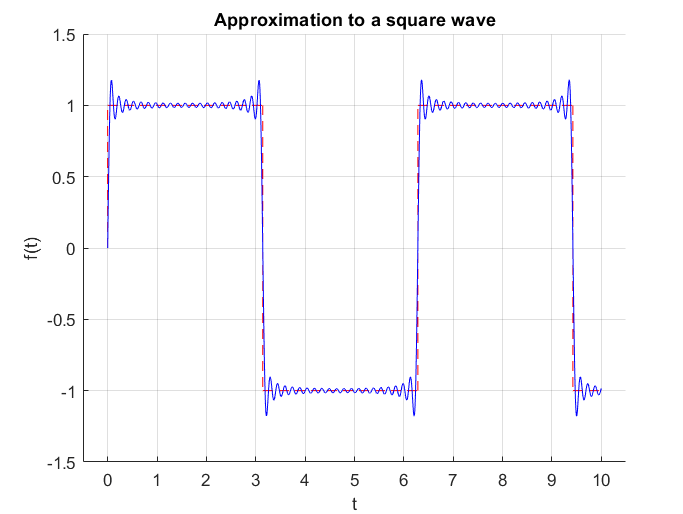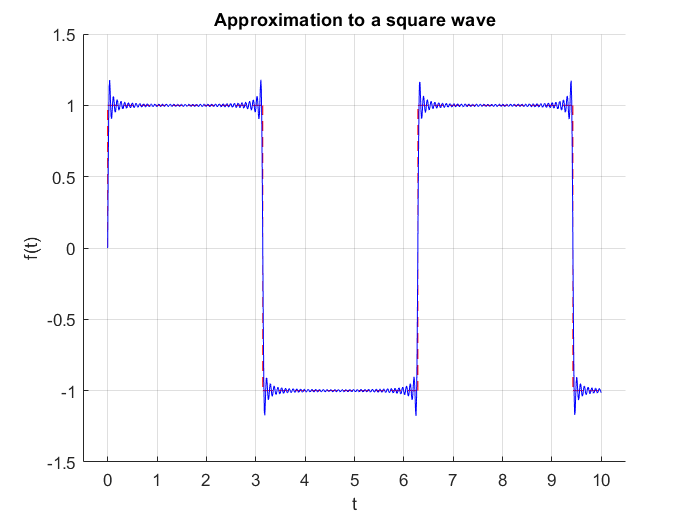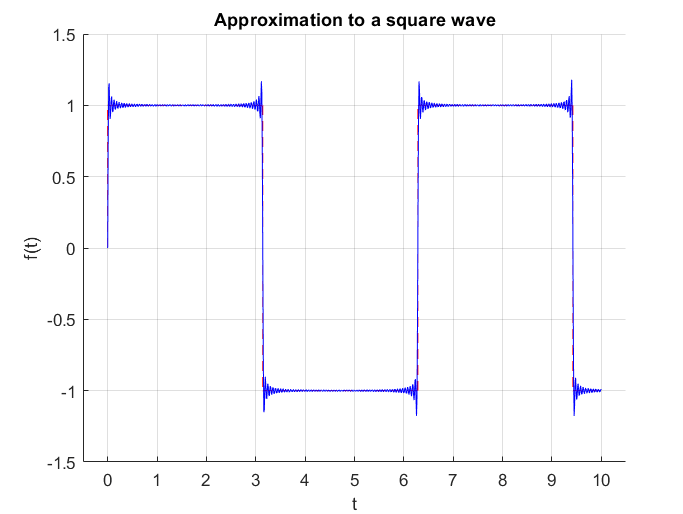
Figure 3. Unlike Taylor series, which approximates a function at a specific point, Fourier series approximates a function within a specific interval.

Utilizing the relationship between function values at a specific point and its surrounding values.

If we carefully consider the equation of Taylor series, we can see that in order to approximate a function at a specific function value, we need to use the function value and the derivative value at that point.

However, if we think about it, the derivative, or the rate of change, represents the relationship between the function value at a specific point and its surrounding function values.

The first derivative represents the relationship with the immediate neighboring point, the second derivative represents the relationship with the points two steps away (or the immediate neighboring point and the second neighboring point), and so on.

Therefore, as the degree of the derivative increases, the approximation of the function becomes more accurate even for points far away from the function value we want to approximate.

In summary, Taylor series can be seen as a method to estimate the function values around a specific point using the derivative information of that point.