When studying statistics, one encounters many new terms, among which are the representative terms of type I error and type II error.

Although there is no specific meaning derived from the numbers, they seem to have been named as type I and type II in order to distinguish them.

Type I error refers to the error that occurs when the null hypothesis is true but is incorrectly rejected.

Type II error refers to the error that occurs when the null hypothesis is false but is not rejected.

Considering these definitions, it seems important to first understand what the “null hypothesis” is exactly before moving on.

Also, let’s explore how to understand the terms “incorrect rejection” and “incorrect acceptance”.

Events and Null Hypothesis

Before talking about type I and type II errors, it is important to understand that all of these concepts are related to hypotheses about events.

In other words, it is important not to forget that what we perform through analysis such as t-tests and ANOVA is hypothesis testing.

However, there is no such thing as a 100% certain hypothesis test. This is because testing is based on probabilities, so there is always a possibility of drawing the wrong conclusion.

So what are we testing hypotheses about? In other words, what can be the thing we are dealing with? Events can be things like “there was a fire in my apartment” or “the result of rolling a die is 1”.

Events don’t necessarily have to be new or unusual. For example, “the result of rolling a die is 1” can also be an event. However, when conducting hypothesis testing, it is often done to verify whether new results are really new. Therefore, most of the events (or examples) dealt with in hypothesis testing may be more likely to be new or unusual.

Therefore, there are only two hypotheses we can make about events. Either the event occurred or it did not.

In daily lives, conversations often focus on the possibility of an event occurring, but in statistics, hypothesis testing often focuses more on the hypothesis that the event did not occur. This is because the main method of hypothesis testing in statistics is to indirectly prove that the event occurred by discovering the fact that the possibility of the event not happening is very low, assuming that the event did not happen.

Therefore, since statistics often focuses more on the hypothesis that the event did not happen, this assumption has been named the “null hypothesis.”

The null hypothesis is a hypothesis that assumes that nothing has happened, hence the word “null” contains the meaning of nothing.

Type I and Type II Errors

Figure 1. There seems to be no better example than a fire alarm system to understand Type I and Type II errors.
Source: Wikipedia Fire Alarm System

Type I Error: False Alarm

As mentioned earlier, the definition of a Type I error is “rejecting the null hypothesis when it is true.” Let’s take a closer look at what this means.

Saying that the null hypothesis is true means that nothing has happened.

In other words, there was no fire in the apartment. However, if we mistakenly reject this and make a false claim that there was a fire, it refers to a case where a fire alarm goes off even though there was no fire.

Therefore, to express this in one word, it is called a False Alarm.

In other words, even though nothing has actually happened, it was rejected (i.e., the alarm went off).

Type II Error: Miss

On the other hand, the definition of a Type II error is “failing to reject the null hypothesis when it is false.” Let’s also take a closer look at the meaning of this statement.

Saying that the null hypothesis is false means that something has actually happened.

In other words, a fire has already occurred in the apartment. However, if we fail to reject this null hypothesis and do not sound the fire alarm, it refers to a case where the alarm does not go off even though there is a fire.

Therefore, to express this in one word, it is called a Miss.

It means that we missed the timing to reject (i.e., sound the alarm) even though something actually happened.

Summary

In summary, the following results can be obtained by summarizing in a table.

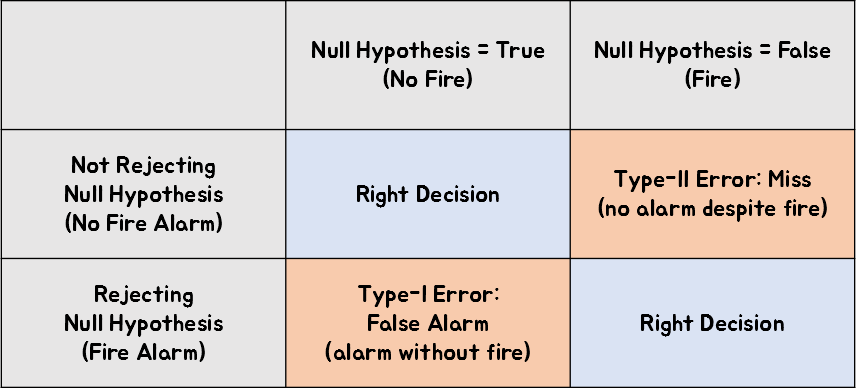
Figure 2. Summary of information on type I and type II errors

Relationship with p-value

Firstly, p-value is related to type I error. We can understand the reason why by reconsidering what p-value is.

This is because p-value means “the probability that the null hypothesis is true when it is assumed to be true”.

In other words, p-value has the same meaning as the probability of committing a type I error.