Prerequisites
To better understand this post, it is recommended to have knowledge about the following:
Starting from the rotation of a circle: sinusoidal waves
A sinusoidal wave refers to a sine wave or a cosine wave. You may remember learning about trigonometry in middle school and trigonometric functions in high school. Sine and cosine waves are included in trigonometric functions.
Looking back, during high school, while trying to apply difficult differential/integral calculus to trigonometric functions, I think I ended up forgetting the essence of sinusoidal waves and only remembered their waveforms and calculation methods.
The essence of sinusoidal waves is related to the rotation of a circle and its description of the rotation over time.
Figure 1. A point on the circle is rotating every 4 seconds.
Note that the direction of rotation is counterclockwise by default. The reason why it was initially defined in this way is unknown, but counterclockwise direction is usually considered as the positive direction.
The circle is located on a 2D plane. However, when trying to describe the rotation over time on a graph, one of the two dimensions on the 2D plane had to be given up.
The easiest way is to describe only the changes on the $x$-axis or $y$-axis of the rotating circle over time.
Figure 2. Observing only the changes on the $x$- and $y$-axes of the point on the circle every 4 seconds.
The idea is to represent the movement on the $x$ or $y$ axis over time shown in the figure below by setting a new time axis.
Figure 3. Representing the change over time of the x-axis and y-axis on a circle as a graph results in a sine wave.
The resulting waveform obtained in this way is two, and the graph of the time variation of the $x$ axis is called a cosine wave, while that of the $y$ axis is called a sine wave.
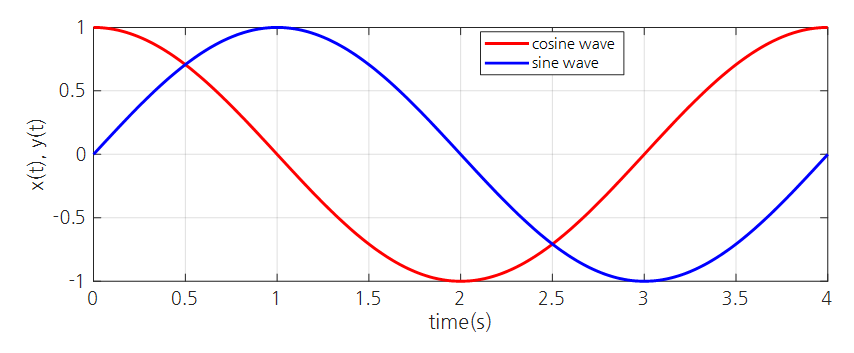
Figure 4. Cosine and sine waves with a period of 4 seconds.
Three characteristics of a sine wave
We have seen that we can think of a sine wave from the rotation of a circle.
Based on this fact, we can imagine some variations in the rotation of a circle.
First, we can modify the radius of the circle, and we can also adjust the rotational speed.
In addition, we can change the position where the rotation begins.
These three are respectively called the amplitude, frequency, and phase shift of the sine wave.
If we use a cosine wave as a reference, the amplitude, frequency, and phase shift are expressed as follows:
\[x(t)=A\cos(2\pi f_0 t+\phi) = A\cos(\omega_0 t + \phi)\]Here, $A$ represents amplitude, $f_0$ represents frequency, $\phi$ represents phase shift, and $\omega_0$ represents the radian frequency.
Let’s take a closer look at this.
Amplitude
Amplitude is not a difficult concept. The amplitude of a sine wave is equal to the length of the radius of a rotating circle.
Figure 5. Rotation of circles with different radii.
Basically, since the cosine function $cos(\theta)$ oscillates between +1 and -1, $A\cos(\theta)$ oscillates between $-A$ and $+A$.
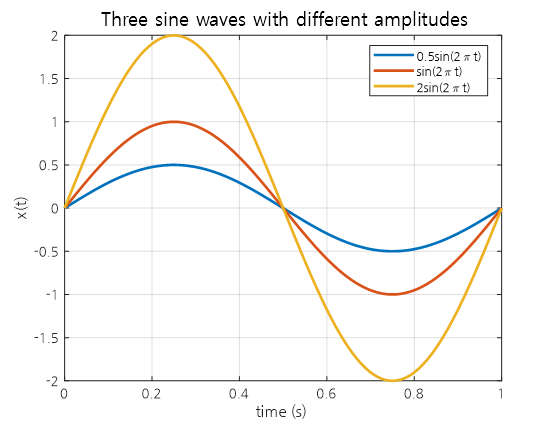
Figure 6. Three sine waves with different amplitudes.
However, when drawing a sine wave, it is often written that the horizontal axis represents time and the vertical axis represents amplitude. It would be good to note that this is not the correct representation.
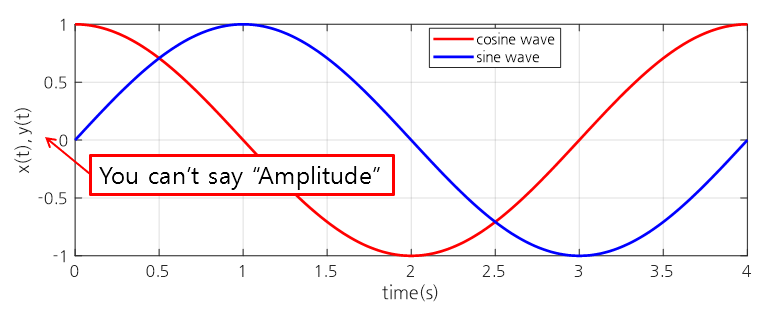
Figure 7. Labeling the vertical axis as amplitude is an incorrect notation.
Frequency
The concept of frequency is related to the speed of rotation. It is about how fast something is rotating.
The higher the frequency, the faster the rotation.
Figure 8. Rotation of circles with different frequencies.
Frequency is the reciprocal of the period and is measured in Hz (Hertz), which means cycles per second.
Therefore, 0.25 Hz means one rotation every 4 seconds, 1 Hz means one rotation per second, and 2 Hz means one rotation every 0.5 seconds.
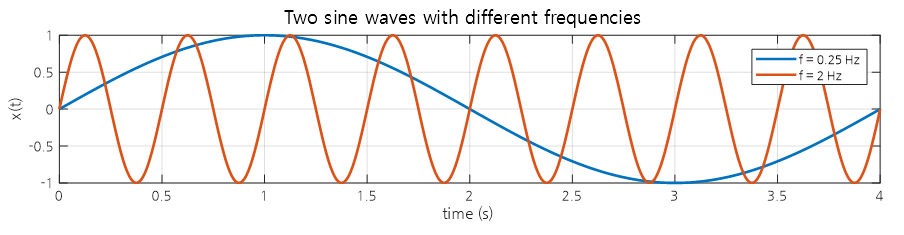
Figure 9. Comparison of sine waves with different frequencies of 0.25 Hz and 2 Hz
One of the concepts that is difficult to understand regarding the frequency of a sinusoidal wave is the radian frequency. Radian frequency is usually denoted by $\omega$ (pronounced “omega”).
The radian angle system is an angle system created by considering that the ratio of the radius to the length of the arc traveled when a circle rotates once is always $2\pi$.
If 1 Hz means one rotation per second, radian frequency is a concept that was created to easily understand how many radians it rotates in one second.
For example, a radian frequency of $2\pi$ rad/s means one rotation per second. However, it expresses how much it has rotated using the radian angle system.
Therefore, if we write the frequency expressed in Hz as $f$ and the radian frequency as $\omega$, we have the following relationship:
\[\omega = 2\pi f\]Phase shift
Many people find it difficult to understand the concept of phase when studying sinusoidal waves.
The term phase is unfamiliar to some because it is often used when studying the moon in earth science.
When a phase shift occurs, the sinusoidal wave shifts to the left or right, as shown in the figure below.
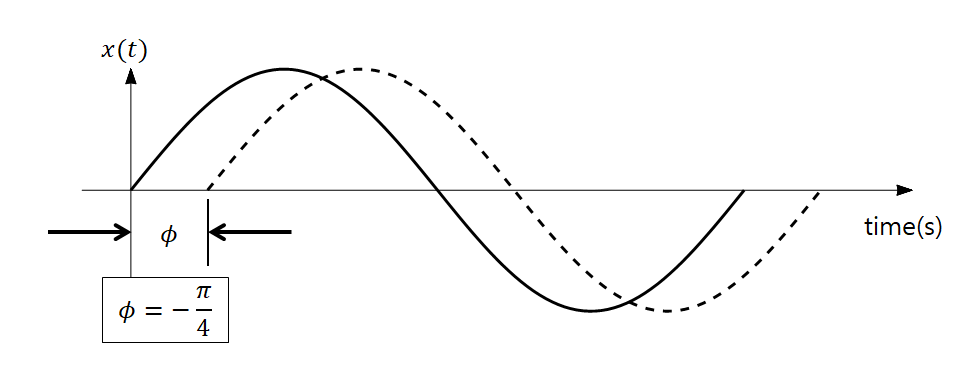
Figure 10. When a phase shift occurs, the sinusoidal wave shifts to the left or right.
If you are confused about the left/right movement, think again about the rotation of the circle, the homeland of the sinusoidal wave.
In other words, the phase indicates “where to start on the circle.”
In other words, in equation (1), $\phi$ is just the starting position of the rotation.
Figure 11. Sine wave display for the rotation of circles with different phase displacements
Therefore, when considering the fact that the phase has been shifted, it is sufficient to think about where to start the rotation from.
However, the part that can be a little confusing is the time delay caused by the phase shift, but if you think about it simply, you can transform equation (1) as follows:
\[\text{Equation (1)} \Rightarrow A\cos\left(2\pi f\left(t+\frac{\phi}{2\pi f}\right)\right)=A\cos\left(2\pi f\left(t-t_d\right)\right)\]That is, if there was a phase shift of $\phi$ radians, the time delay $t_d$ caused by it can be expressed as:
\[t_d = -\frac{\phi}{2\pi f}\]in seconds.